若实数 $x,y$ 满足 ${\begin{cases}
x + 2y - 4 \leqslant 0 ,\\
x - y - 1 \leqslant 0 ,\\
x \geqslant 1, \\
\end{cases}}$ 则 $x + y$ 的取值范围是 ．
x + 2y - 4 \leqslant 0 ,\\
x - y - 1 \leqslant 0 ,\\
x \geqslant 1, \\
\end{cases}}$ 则 $x + y$ 的取值范围是
【难度】
【出处】
2014年高考浙江卷（文）
【标注】
【答案】
$\left[1,3\right]$
【解析】
本题是一道线性规划问题，做出可行域，求目标函数的取值范围．$x$，$y$ 满足的区域如图所示，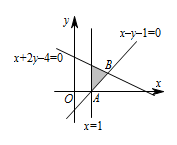
令 $z=x+y$，显然当直线 $z=x+y$ 经过 $B\left(2,1\right)$ 时，$z$ 取得最大值 $3$；经过 $A\left(1,0\right)$ 时，$z$ 取得最小值 $1$．
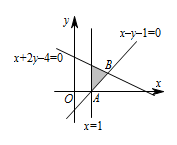令 $z=x+y$，显然当直线 $z=x+y$ 经过 $B\left(2,1\right)$ 时，$z$ 取得最大值 $3$；经过 $A\left(1,0\right)$ 时，$z$ 取得最小值 $1$．
题目
答案
解析
备注
