2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为 $8848.86$(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现在 $A,B,C$ 三点,且 $A,B,C$ 在同一水平面上的投影 $A',B',C'$ 满足 $\angle A'C'B'=45^{\circ}, \angle A'B'C'=60^{\circ}$.由 $C$ 点测得 $B$ 点的仰角为 $15^{\circ}$,$BB'$ 与 $CC'$ 的差为 $100$:由 $B$ 点测得 $A$ 点的仰角为 $45^{\circ}$,则 $A,C$ 两点到水平面 $A'B'C'$ 的高度差 $AA'-CC'$ 约为($\sqrt{3}\approx 1.732$) \((\qquad)\) .

【难度】
【出处】
无
【标注】
【答案】
B
【解析】
过 $C$ 作 $BB'$ 垂线,垂足为 $M$,过 $B$ 作 $AA'$ 垂线,垂足为 $N$.由题意得 $BM=100, \angle BCM=15^{\circ}, \angle ABN=45^{\circ}$,即 $CM=\frac{100\sin 75^{\circ}}{\sin 15^{\circ}}=B'C'$.
所以$$BN=B'A'=\frac{B'C'\sin 45^{\circ}}{\sin 75^{\circ}}=\frac{100\sin 75^{\circ}\sin 45^{\circ}}{\sin 75^{\circ}\sin 15^{\circ}}=\frac{50\sqrt{2}}{\sin 15^{\circ}}.$$所以$$AN=BN=\frac{50\sqrt{2}}{\sin15^{\circ}}=\frac{50\sqrt{2}}{\frac{\sqrt{6}-\sqrt{2}}{4}}=273.$$所以 $AA'-CC'=AN+BM=273+100=373$.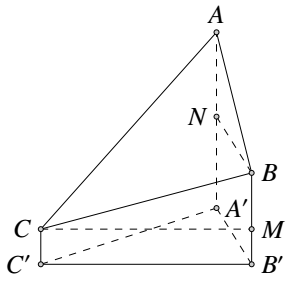
所以$$BN=B'A'=\frac{B'C'\sin 45^{\circ}}{\sin 75^{\circ}}=\frac{100\sin 75^{\circ}\sin 45^{\circ}}{\sin 75^{\circ}\sin 15^{\circ}}=\frac{50\sqrt{2}}{\sin 15^{\circ}}.$$所以$$AN=BN=\frac{50\sqrt{2}}{\sin15^{\circ}}=\frac{50\sqrt{2}}{\frac{\sqrt{6}-\sqrt{2}}{4}}=273.$$所以 $AA'-CC'=AN+BM=273+100=373$.

题目
答案
解析
备注