已知 $A,B,C$ 是半径为 $1$ 的球 $O$ 的球面上的三个点，且 $AC\perp BC, AC=BC=1$，则三棱锥 $O-ABC$ 的体积为 \((\qquad)\) ．
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
记 $O'$ 为 $A,B,C$ 所在圆面的圆心，则 $OO'\perp \triangle ABC$．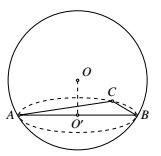
又 $AB=\sqrt{2}$，所以$$OO'=\sqrt{OA^2-AO'^2}=\sqrt{1^2-\left(\frac{\sqrt{2}}{2}\right)^2}=\frac{\sqrt{2}}{2}.$$所以$$V_{O-ABC}=\frac{1}{3}\cdot S_{\triangle ABC}\cdot OO'=\frac{1}{3}\cdot \frac{1}{2}\cdot 1\cdot 1\cdot \frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{12}.$$故选A．
又 $AB=\sqrt{2}$，所以$$OO'=\sqrt{OA^2-AO'^2}=\sqrt{1^2-\left(\frac{\sqrt{2}}{2}\right)^2}=\frac{\sqrt{2}}{2}.$$所以$$V_{O-ABC}=\frac{1}{3}\cdot S_{\triangle ABC}\cdot OO'=\frac{1}{3}\cdot \frac{1}{2}\cdot 1\cdot 1\cdot \frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{12}.$$故选A．
题目
答案
解析
备注
