已知 $F $ 为双曲线 $C:\dfrac{x^2}
{9} - \dfrac{y^2}
{16} = 1$ 的左焦点,$P,Q $ 为 $C $ 上的点.若 $PQ $ 的长等于虚轴长的 $ 2 $ 倍,点 $A\left(5,0\right) $ 在线段 $PQ $ 上,则 $\triangle PQF $ 的周长为 .
{9} - \dfrac{y^2}
{16} = 1$ 的左焦点,$P,Q $ 为 $C $ 上的点.若 $PQ $ 的长等于虚轴长的 $ 2 $ 倍,点 $A\left(5,0\right) $ 在线段 $PQ $ 上,则 $\triangle PQF $ 的周长为
【难度】
【出处】
2013年高考辽宁卷(文)
【标注】
【答案】
$ 44 $
【解析】
点 $P,Q$ 均与双曲线的两焦点有关,从双曲线的定义角度考虑即可.由题意,得 $|PQ|=16 $,且线段 $PQ $ 过双曲线的右焦点,$P,Q $ 都在双曲线的右支上.
由双曲线的定义,可知\[|PF| - |PA| = 2a, |QF| - |QA| = 2a,\]两式相加,得\[|PF| + |QF| - \left(|PA| + |QA|\right) = 4a.\]则\[|PF| + |QF| = 4a + |PQ| = 28.\]故 $\triangle PQF $ 的周长为 $ 44$.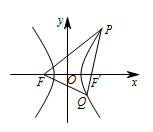
由双曲线的定义,可知\[|PF| - |PA| = 2a, |QF| - |QA| = 2a,\]两式相加,得\[|PF| + |QF| - \left(|PA| + |QA|\right) = 4a.\]则\[|PF| + |QF| = 4a + |PQ| = 28.\]故 $\triangle PQF $ 的周长为 $ 44$.

题目
答案
解析
备注