在 $OA$ 为边、$OB$ 为对角线的矩形中，已知 $\overrightarrow {OA} = \left( - 3,1 \right)$，$\overrightarrow {OB} = \left( - 2,k \right)$，则实数 $k = $ ．
【难度】
【出处】
2013年高考重庆卷（文）
【标注】
【答案】
$ 4 $
【解析】
本题考查平面向量的数量积的坐标运算．根据平面向量的数量积得\[\overrightarrow{OA}\cdot\overrightarrow{OB}=|\overrightarrow{OA}|\times \left|\overrightarrow{OB}\right|\cos\left\langle \overrightarrow{OA},\overrightarrow{OB }\right\rangle =\left|\overrightarrow {OA}\right|^2,\]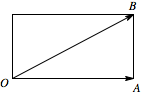
因为 $\overrightarrow {OA}\cdot \overrightarrow {OB}=6+k$，$\left|\overrightarrow{OA}\right|^2=10$，所以 $6+k=10$，$k=4$．
因为 $\overrightarrow {OA}\cdot \overrightarrow {OB}=6+k$，$\left|\overrightarrow{OA}\right|^2=10$，所以 $6+k=10$，$k=4$．
题目
答案
解析
备注
