已知点 $A\left(1, - 1\right),B\left(3,0\right),C\left(2,1\right)$．若平面区域 $D$ 由所有满足 $\overrightarrow {AP} = \lambda \overrightarrow {AB} + \mu \overrightarrow {AC} \left(1 \leqslant \lambda \leqslant 2,0 \leqslant \mu \leqslant 1\right)$ 的点 $P$ 组成，则 $D$ 的面积为 ．
【难度】
【出处】
2013年高考北京卷（文）
【标注】
【答案】
$ 3$
【解析】
根据题中向量关系式，得出点 $P$ 的横纵坐标满足的关系式，根据线性规划对出面积即可．设 $P\left(x,y\right)$，则由平面向量的坐标运算得\[\overrightarrow {AP} = \left(x - 1,y + 1\right).\]由题意知 $\overrightarrow {AB} = \left(2,1\right),\overrightarrow {AC} = \left(1,2\right)$．由 $\overrightarrow {AP} = \lambda \overrightarrow {AB} + \mu \overrightarrow {AC} $ 得\[\left(x- 1,y + 1\right) = \lambda \left(2,1\right) + \mu \left(1,2\right),\]即\[{\begin{cases}
2\lambda + \mu = x - 1, \\
\lambda + 2\mu = y + 1. \\
\end{cases}}\]所以\[{\begin{cases}\lambda = \dfrac{2x - y - 3}{3}, \\
\mu = \dfrac{2y - x + 3}{3}, \\
\end{cases}}\]所以 $1 \leqslant \lambda \leqslant 2$，$0 \leqslant \mu \leqslant 1$，所以\[{\begin{cases}3 \leqslant 2x - y - 3 \leqslant 6, \\
0 \leqslant 2y - x + 3 \leqslant 3. \\
\end{cases}}\]不等式组所表示的平面区域如图阴影部分所示：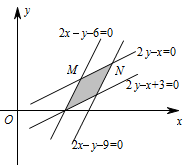
由图可知平面区域 $D$ 为平行四边形，可求出 $M\left(4,2\right)$，$N\left(6,3\right)$，故 $|MN| = \sqrt 5 $．又 $x - 2y = 0$ 与 $x - 2y - 3 = 0$ 之间的距离为 $d = \dfrac{3}{\sqrt 5 }$，故平面区域 $D$ 的面积为 $S = \sqrt 5 \times \dfrac{3}{\sqrt 5 } = 3$．
2\lambda + \mu = x - 1, \\
\lambda + 2\mu = y + 1. \\
\end{cases}}\]所以\[{\begin{cases}\lambda = \dfrac{2x - y - 3}{3}, \\
\mu = \dfrac{2y - x + 3}{3}, \\
\end{cases}}\]所以 $1 \leqslant \lambda \leqslant 2$，$0 \leqslant \mu \leqslant 1$，所以\[{\begin{cases}3 \leqslant 2x - y - 3 \leqslant 6, \\
0 \leqslant 2y - x + 3 \leqslant 3. \\
\end{cases}}\]不等式组所表示的平面区域如图阴影部分所示：
由图可知平面区域 $D$ 为平行四边形，可求出 $M\left(4,2\right)$，$N\left(6,3\right)$，故 $|MN| = \sqrt 5 $．又 $x - 2y = 0$ 与 $x - 2y - 3 = 0$ 之间的距离为 $d = \dfrac{3}{\sqrt 5 }$，故平面区域 $D$ 的面积为 $S = \sqrt 5 \times \dfrac{3}{\sqrt 5 } = 3$．
题目
答案
解析
备注
