已知圆 $O$ 和圆 $K$ 是球 $O$ 的大圆和小圆,其公共弦长等于球 $O$ 的半径,$OK = \dfrac{3}{2}$,且圆 $O$ 与圆 $K$ 所在的平面所成的一个二面角为 $60^\circ $,则球 $O$ 的表面积等于 .
【难度】
【出处】
无
【标注】
【答案】
$16{\mathrm \pi} $
【解析】
本题考查球中的大圆与小圆问题,注意到球心与圆心连线垂直于圆面,圆心与弦中点的连线垂直于弦.如图所示,公共弦为 $AB$,设球的半径为 $R$,则 $AB = R$.
取 $AB$ 中点 $M$,连接 $OM$,$KM$,由圆的性质知 $OM \perp AB$,$KM \perp AB$,所以 $\angle KMO$ 为圆 $O$ 与圆 $K$ 所在平面所成的二面角的平面角,则 $\angle KMO = 60^\circ $.
在 ${\mathrm{Rt}}\triangle KMO$ 中,$OK = \dfrac{3}{2}$,所以 $OM = \dfrac{OK}{\sin 60^\circ } = \sqrt 3. $
在 ${\mathrm{Rt}}\triangle OAM$ 中,因为 $O{A^2} = O{M^2} + A{M^2}$,所以 ${R^2} = 3 + \dfrac{1}{4}{R^2},$
解得 ${R^2} = 4$,所以球 $O$ 的表面积为 $4{\mathrm \pi} {R^2} = 16{\mathrm \pi} $.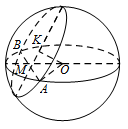
取 $AB$ 中点 $M$,连接 $OM$,$KM$,由圆的性质知 $OM \perp AB$,$KM \perp AB$,所以 $\angle KMO$ 为圆 $O$ 与圆 $K$ 所在平面所成的二面角的平面角,则 $\angle KMO = 60^\circ $.
在 ${\mathrm{Rt}}\triangle KMO$ 中,$OK = \dfrac{3}{2}$,所以 $OM = \dfrac{OK}{\sin 60^\circ } = \sqrt 3. $
在 ${\mathrm{Rt}}\triangle OAM$ 中,因为 $O{A^2} = O{M^2} + A{M^2}$,所以 ${R^2} = 3 + \dfrac{1}{4}{R^2},$
解得 ${R^2} = 4$,所以球 $O$ 的表面积为 $4{\mathrm \pi} {R^2} = 16{\mathrm \pi} $.

题目
答案
解析
备注