已知函数 $f\left(x\right)=\begin{cases}
x^3,&x\leqslant a,\\
x^2,&x>a
\end{cases}$,若存在实数 $b$,使函数 $g\left(x\right)=f\left(x\right)-b$ 有两个零点,则 $a$ 的取值范围是 .
x^3,&x\leqslant a,\\
x^2,&x>a
\end{cases}$,若存在实数 $b$,使函数 $g\left(x\right)=f\left(x\right)-b$ 有两个零点,则 $a$ 的取值范围是
【难度】
【出处】
无
【标注】
【答案】
$\left(-\infty,0\right)\cup \left(1,+\infty\right)$
【解析】
根据 $a$ 的值与 $0$ 和 $1$ 的关系,分别画出分段函数的图象,观察得出答案.函数 $y=x^3$ 和 $y=x^2$ 都是幂函数,这道题可以结合这两个函数的特点,借助函数的图象来分析.
使函数 $g\left(x\right)=f\left(x\right)-b$ 有两个零点,则需 $y=f\left(x\right)$ 和 $y=b$ 有两个交点,如图所示,当 $a<0$ 或 $a>1$ 时,存在实数 $b$,使它们有两个交点.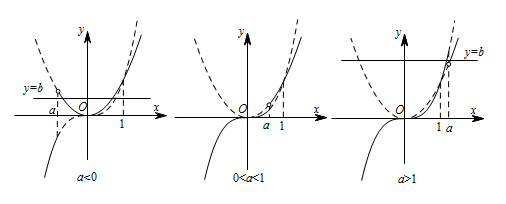
使函数 $g\left(x\right)=f\left(x\right)-b$ 有两个零点,则需 $y=f\left(x\right)$ 和 $y=b$ 有两个交点,如图所示,当 $a<0$ 或 $a>1$ 时,存在实数 $b$,使它们有两个交点.

题目
答案
解析
备注