设 $x$，$y$ 满足约束条件 ${\begin{cases}
1 \leqslant x \leqslant 3, \\
- 1 \leqslant x - y \leqslant 0, \\
\end{cases}}$ 则 $z = 2x - y$ 的最大值为 ．
1 \leqslant x \leqslant 3, \\
- 1 \leqslant x - y \leqslant 0, \\
\end{cases}}$ 则 $z = 2x - y$ 的最大值为
【难度】
【出处】
2013年高考新课标I卷（文）
【标注】
【答案】
$ 3 $
【解析】
本题考查线性规划相关知识．作出可行域，将目标函数转化为直线 $y=2x-z$，只要求纵截距 $-z$ 的最小值即可．画出可行域：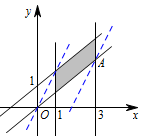
当目标函数的图象经过点 $ A\left(3,3\right) $ 时，$ z $ 取得最大值 $ 3 $．
当目标函数的图象经过点 $ A\left(3,3\right) $ 时，$ z $ 取得最大值 $ 3 $．
题目
答案
解析
备注
