已知 $H$ 是球 $O$ 的直径 $AB$ 上一点，$AH:HB = 1:2$，$AB \perp $ 平面 $\alpha $，$H$ 为垂足，平面 $\alpha $ 截球 $O$ 所得截面的面积为 ${\mathrm \pi} $，则球 $O$ 的表面积为 ．
【难度】
【出处】
2013年高考新课标I卷（文）
【标注】
【答案】
$\dfrac{9}{2}{\mathrm \pi} $
【解析】
本题考查球的表面积计算，结合条件计算球的半径是解题关键．如图，设球 $O$ 的半径为 $R$．因为 $AH:HB = 1:2$，所以 $OH=\dfrac13R$．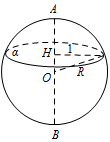
由题意可得平面 $\alpha $ 截球 $O$ 所得截面圆的半径为 $1$．故\[\left(\dfrac13R\right)^2+1^2=R^2,\]解得 $R^2=\dfrac98$．所以球 $O$ 的表面积为 $4{\mathrm \pi} R^2=\dfrac{9}{2}{\mathrm \pi} $．
由题意可得平面 $\alpha $ 截球 $O$ 所得截面圆的半径为 $1$．故\[\left(\dfrac13R\right)^2+1^2=R^2,\]解得 $R^2=\dfrac98$．所以球 $O$ 的表面积为 $4{\mathrm \pi} R^2=\dfrac{9}{2}{\mathrm \pi} $．
题目
答案
解析
备注
