已知正四棱锥 $O - ABCD$ 的体积为 $\dfrac{3\sqrt 2 }{2}$，底面边长为 $\sqrt 3 $，则以 $O$ 为球心，$OA$ 为半径的球的表面积为 ．
【难度】
【出处】
2013年高考新课标Ⅱ卷（文）
【标注】
【答案】
$24{\mathrm \pi} $
【解析】
利用已知条件，结合勾股定理求解棱长 $OA$ 为解题关键．如图：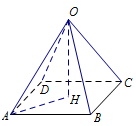
由已知和棱锥的体积公式得正四棱锥 $O - ABCD$ 的高 $OH$ 为 $\dfrac{3\sqrt 2 }{2}$．
又 $AH=\dfrac{\sqrt 6 }{2}$，所以 $OA=\sqrt 6 $．故所求球的表面积为 $24{\mathrm \pi} $．
由已知和棱锥的体积公式得正四棱锥 $O - ABCD$ 的高 $OH$ 为 $\dfrac{3\sqrt 2 }{2}$．又 $AH=\dfrac{\sqrt 6 }{2}$，所以 $OA=\sqrt 6 $．故所求球的表面积为 $24{\mathrm \pi} $．
题目
答案
解析
备注
