已知函数 $f\left( x \right) = \left| {{x^2} + 3x} \right|$,$x \in{\mathbb { R}}$.若方程 $f\left( x \right) - a\left| {x - 1} \right| = 0$ 恰有 $ 4 $ 个互异的实数根,则实数 $a$ 的取值范围为 .
【难度】
【出处】
无
【标注】
【答案】
$\left(0,1\right)\cup \left(9,+\infty\right) $
【解析】
直接求解方程的根比较困难,故可以通过对参数全分离或半分离的代数变形,将方程的根转化为函数的交点问题.当 $x=1 $ 时,方程不成立.
当 $x \ne 1$ 时,$a = \left| {\dfrac{{{x^2} + 3x}}{x - 1}} \right|$,令 $t = x - 1$,则 $a = \left| {t + \dfrac{4}{t} + 5} \right|$.
因为 $t + \dfrac{4}{t} \in \left( { - \infty , - 4} \right] \cup \left[ {4, + \infty } \right)$,所以 $t + \dfrac{4}{t} + 5 \in \left( { - \infty ,1} \right] \cup \left[ {9, + \infty } \right)$,
考虑到函数 $y = \left| {t + \dfrac{4}{t} + 5} \right|$和 $ y=a$ 的图象(如图)有四个交点,可得 $0 < a < 1$ 或 $ a > 9$.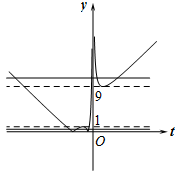
当 $x \ne 1$ 时,$a = \left| {\dfrac{{{x^2} + 3x}}{x - 1}} \right|$,令 $t = x - 1$,则 $a = \left| {t + \dfrac{4}{t} + 5} \right|$.
因为 $t + \dfrac{4}{t} \in \left( { - \infty , - 4} \right] \cup \left[ {4, + \infty } \right)$,所以 $t + \dfrac{4}{t} + 5 \in \left( { - \infty ,1} \right] \cup \left[ {9, + \infty } \right)$,
考虑到函数 $y = \left| {t + \dfrac{4}{t} + 5} \right|$和 $ y=a$ 的图象(如图)有四个交点,可得 $0 < a < 1$ 或 $ a > 9$.

题目
答案
解析
备注