已知菱形 $ABCD$ 的边长为 $2$，$\angle BAD = {120^ \circ }$，点 $E$，$F$ 分别在边 $BC$，$DC$ 上，$BC = 3BE$，$DC = \lambda DF$．若 $\overrightarrow {AE} \cdot \overrightarrow {AF} = 1$，则 $\lambda $ 的值为 ．
【难度】
【出处】
2014年高考天津卷（文）
【标注】
【答案】
$ 2 $
【解析】
本题是对向量分解与数量积的综合考查，根据题中的条件，我们可以选择 $\overrightarrow {AD}$ 与 $\overrightarrow{AB}$ 为一组基底，然后再结合数量积公式，问题即可解决．如图：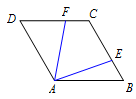
由题意及平面向量的加减法得\[\begin{split}\overrightarrow {AE}\cdot \overrightarrow{AF}&=\left(\overrightarrow {AB}+\overrightarrow {BE}\right)\cdot \left(\overrightarrow {AD}+\overrightarrow {DF}\right)\\&=\left(\overrightarrow {AB}+\dfrac 13\overrightarrow {AD}\right)\cdot \left(\overrightarrow {AD}+\dfrac 1{\lambda}\overrightarrow {AB}\right).\end{split}\]由平面向量的数量积展开化简得\[\overrightarrow {AE}\cdot \overrightarrow{AF}=\dfrac{10}{3\lambda}-\dfrac23,\]又因为 $\overrightarrow {AE}\cdot \overrightarrow{AF}=1$，所以 $\dfrac{10}{3\lambda}-\dfrac23 =1$，解得 $\lambda=2$．
由题意及平面向量的加减法得\[\begin{split}\overrightarrow {AE}\cdot \overrightarrow{AF}&=\left(\overrightarrow {AB}+\overrightarrow {BE}\right)\cdot \left(\overrightarrow {AD}+\overrightarrow {DF}\right)\\&=\left(\overrightarrow {AB}+\dfrac 13\overrightarrow {AD}\right)\cdot \left(\overrightarrow {AD}+\dfrac 1{\lambda}\overrightarrow {AB}\right).\end{split}\]由平面向量的数量积展开化简得\[\overrightarrow {AE}\cdot \overrightarrow{AF}=\dfrac{10}{3\lambda}-\dfrac23,\]又因为 $\overrightarrow {AE}\cdot \overrightarrow{AF}=1$，所以 $\dfrac{10}{3\lambda}-\dfrac23 =1$，解得 $\lambda=2$．
题目
答案
解析
备注
