已知函数 $f\left(x\right) = \begin{cases}
\left| {{x^2} + 5x + 4} \right|,&x \leqslant 0 ,\\
2\left| {x - 2} \right|,&x > 0, \\
\end{cases}$ 若函数 $y = f\left(x\right) - a\left| x \right|$ 恰有 $ 4 $ 个零点，则实数 $a$ 的取值范围为 ．
\left| {{x^2} + 5x + 4} \right|,&x \leqslant 0 ,\\
2\left| {x - 2} \right|,&x > 0, \\
\end{cases}$ 若函数 $y = f\left(x\right) - a\left| x \right|$ 恰有 $ 4 $ 个零点，则实数 $a$ 的取值范围为
【难度】
【出处】
无
【标注】
【答案】
$\left(1,2\right)$
【解析】
直接研究 $y=f\left(x\right)-a|x|$ 的零点比较困难，因此可以将问题转化为 $y=f\left(x\right)$ 与 $y=a|x|$ 的交点，然后结合图象解决问题．考查函数 $ y=f\left(x\right)$ 图象与 $ y=a|x|$ 图象的交点的情况，根据图象，得 $a>0 $．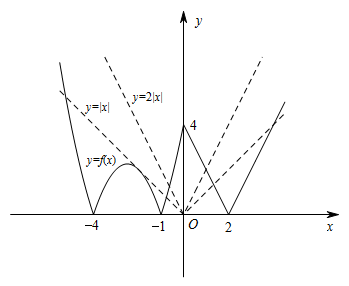
当 $a=2 $ 时，函数 $ y=f\left(x\right)$ 与 $ y=a|x|$ 图象有 $ 3 $ 个交点；
当 $ y=a|x|\left(x\leqslant 0\right)$ 图象与 $y = \left| {{x^2} + 5x + 4} \right|$ 图象相切时，在整个定义域内，函数 $ y=f\left(x\right)$ 图象与 $ y=a|x|$ 图象有 $ 5 $ 个交点，
此时，由 $\begin{cases} y=-ax,\\y=-x^2-5x-4,\end{cases}$ 得 ${x^2} + \left( {5 - a} \right)x + 4 = 0$．
由 $\Delta=0 $，解得 $a=1 $ 或 $ a=9$（舍去）．
故当 $ 1<a<2$ 时，函数 $ y=f\left(x\right)$ 与 $ y=a|x|$ 图象有 $ 4 $ 个交点，即函数 $y = f\left(x\right) - a\left| x \right|$ 恰有 $ 4 $ 个零点．
当 $a=2 $ 时，函数 $ y=f\left(x\right)$ 与 $ y=a|x|$ 图象有 $ 3 $ 个交点；当 $ y=a|x|\left(x\leqslant 0\right)$ 图象与 $y = \left| {{x^2} + 5x + 4} \right|$ 图象相切时，在整个定义域内，函数 $ y=f\left(x\right)$ 图象与 $ y=a|x|$ 图象有 $ 5 $ 个交点，
此时，由 $\begin{cases} y=-ax,\\y=-x^2-5x-4,\end{cases}$ 得 ${x^2} + \left( {5 - a} \right)x + 4 = 0$．
由 $\Delta=0 $，解得 $a=1 $ 或 $ a=9$（舍去）．
故当 $ 1<a<2$ 时，函数 $ y=f\left(x\right)$ 与 $ y=a|x|$ 图象有 $ 4 $ 个交点，即函数 $y = f\left(x\right) - a\left| x \right|$ 恰有 $ 4 $ 个零点．
题目
答案
解析
备注
