若变量 $x , y$ 满足约束条件 $\begin{cases}
{y \leqslant x} ,\\
{x + y \leqslant 4}, \\
{y \geqslant 1},
\end{cases}$ 则 $z = 2x + y$ 的最大值为 ．
{y \leqslant x} ,\\
{x + y \leqslant 4}, \\
{y \geqslant 1},
\end{cases}$ 则 $z = 2x + y$ 的最大值为
【难度】
【出处】
2014年高考湖南卷（文）
【标注】
【答案】
$ 7 $
【解析】
首先画出可行域，然后将目标函数看成直线，只需求解其纵截距 $z$ 的最大值即可．变量 $x,y$ 满足的可行域，如图阴影部分所示．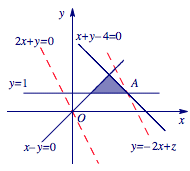
目标函数 $z=2x+y$ 可变形为 $y=-2x+z$，$z$ 表示直线 $y=-2x+z$ 的纵截距，当直线经过点 $A$ 时，直线的纵截距最大，因此，此时 $z=2x+y$ 取得最大值为 $7$．
目标函数 $z=2x+y$ 可变形为 $y=-2x+z$，$z$ 表示直线 $y=-2x+z$ 的纵截距，当直线经过点 $A$ 时，直线的纵截距最大，因此，此时 $z=2x+y$ 取得最大值为 $7$．
题目
答案
解析
备注
