在平面四边形 $ABCD$ 中，$\angle A=\angle B=\angle C=75^\circ$，$BC=2$，则 $AB$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left(\sqrt 6-\sqrt 2,\sqrt 6+\sqrt 2\right)$
【解析】
注意到此四边形四个内角确定，且知道其中一边长度，则可以考虑极限状态下，即四边形退化为三角形时得到线段 $AB$ 的长度即所求范围之极限．延长 $BA$，$CD$，交于点 $A_2$，作 $CA_1\parallel DA$ 交 $AB$ 于点 $A_1$，则 $BA_1<BA<BA_2$．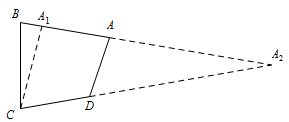
在 $\triangle A_1BC$ 中，由正弦定理$\dfrac {BC}{\sin \angle BA_1C}=\dfrac {BA_1}{\sin \angle BCA_1}$，求得 $BA_1=\sqrt 6-\sqrt 2$；
在 $\triangle A_2BC$ 中，由正弦定理$\dfrac {BA_2}{\sin \angle BCD}=\dfrac {BC}{\sin \angle A_2}$，求得 $BA_2=\sqrt 6+\sqrt 2$．
所以，$AB$ 的取值范围为 $\left(\sqrt 6-\sqrt 2,\sqrt 6+\sqrt 2\right)$．
在 $\triangle A_1BC$ 中，由正弦定理$\dfrac {BC}{\sin \angle BA_1C}=\dfrac {BA_1}{\sin \angle BCA_1}$，求得 $BA_1=\sqrt 6-\sqrt 2$；在 $\triangle A_2BC$ 中，由正弦定理$\dfrac {BA_2}{\sin \angle BCD}=\dfrac {BC}{\sin \angle A_2}$，求得 $BA_2=\sqrt 6+\sqrt 2$．
所以，$AB$ 的取值范围为 $\left(\sqrt 6-\sqrt 2,\sqrt 6+\sqrt 2\right)$．
题目
答案
解析
备注
