在 $\triangle ABC$ 中,$B=120^\circ$,$AB=\sqrt 2$,$A$ 的角平分线 $AD=\sqrt 3$,则 $AC=$ .
【难度】
【出处】
无
【标注】
【答案】
$ \sqrt 6 $
【解析】
首先解 $\triangle ABD$,求出 $\angle BAD$,则 $\angle BAC$ 的大小可得.然后在 $\triangle ABC$ 中解出 $AC$ 长.在三角形 $ABD$ 中,由正弦定理得,$\dfrac{AD}{\sin B}=\dfrac{AB}{\sin\angle ADB}$,将题中条件代入解得 $\sin\angle ADB=\dfrac{\sqrt 2}{2}$,因为 $0<\angle ADB<60^{\circ}$,所以 $\angle ADB=45^\circ$,所以 $\angle BAD=15^\circ$,所以 $\angle BAC=30^\circ$,所以 $\angle BCA=30^\circ$.在三角形 $ABC$ 中,由正弦定理得,$\dfrac{\sin\angle ABC}{AC}=\dfrac{\sin\angle BCA}{AB}$,解得 $AC=\sqrt 6$.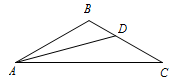

题目
答案
解析
备注