已知直线 $x-y+a=0$ 与圆心为 $ C $ 的圆 $ x^2+y^2+2x-4y-4=0$ 相交于 $A$，$B $ 两点，且 $ AC\perp BC$，则实数 $ a$ 的值为 ．
【难度】
【出处】
2014年高考重庆卷（文）
【标注】
【答案】
$ 0$ 或 $ 6 $．
【解析】
本题是直线与圆相交的问题，可在由弦心距，半径，半弦长构成的直角三角形中解决．由题意，这个三角形是等腰直角三角形．可求得圆 $x^2+y^2-2x-4y-4=0$ 的半径为 $r=3$，因为 $AC\perp BC$，所以圆心 $C$ 到直线 $x-y+a=0$ 的距离为 $\dfrac {\sqrt 2}2r=\dfrac {3\sqrt 2}2$．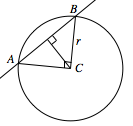
根据点到直线距离公式得\[\dfrac {\left|-3+a\right|}{\sqrt 2}=\dfrac {3\sqrt 2}2,\]解得 $a=0$ 或 $a=6$．
根据点到直线距离公式得\[\dfrac {\left|-3+a\right|}{\sqrt 2}=\dfrac {3\sqrt 2}2,\]解得 $a=0$ 或 $a=6$．
题目
答案
解析
备注
