某校早上 $ 8:00 $ 开始上课,假设该校学生小张与小王在早上 $ 7:30 $ ~ $7:50 $ 之间到校,且每人在该时间段的任何时刻到校是等可能的,则小张比小王至少早 $ 5 $ 分钟到校的概率为 .(用数字作答)
【难度】
【出处】
2014年高考重庆卷(文)
【标注】
【答案】
$\dfrac{9}{32}$
【解析】
本题可设小王、小张的到校时间分别为 $x,y$,然后分析点 $(x,y)$ 在平面坐标系中形成的区域,通过几何概型求解.将 $7:30$ 记为 $0$ 时,则 $7:50$ 为 $20$ 分.设小王和小张到校时间分别为 $x$ 和 $y$(单位:分).则 $\begin{cases}0\leqslant x\leqslant 20,\\ 0\leqslant y\leqslant 20,\end{cases}$ 小张比小王至少早 $5$ 分钟,可表达为 $y\leqslant x-5$.所以,所求概率为图中阴影面积与正方形面积的比值.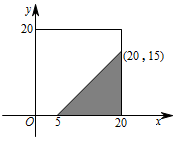

题目
答案
解析
备注