已知直线 $ax + y - 2 = 0$ 与圆心为 $C$ 的圆 ${\left( {x - 1} \right)^2} + {\left( {y - a} \right)^2} = 4$ 相交于 $A$，$B$ 两点，且 $\triangle ABC$ 为等边三角形，则实数 $a = $ ．
【难度】
【出处】
无
【标注】
【答案】
$4 \pm \sqrt {15} $
【解析】
直线与圆相交的问题一般通过弦心距、半径、半弦长所构成的直角三角形解决．若 $\triangle ABC$ 为等边三角形，则圆心到直线的距离 $ d=\dfrac {\sqrt 3}{2}r =\sqrt 3$．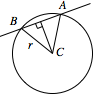
圆心 $ \left(1,a\right)$ 到直线 $ax+y-2=0$ 的距离为 $\dfrac {\left|2a-2\right|}{\sqrt {a^2+1}}$，所以\[\dfrac {\left|2a-2\right|}{\sqrt {a^2+1}}=\sqrt 3,\]解得 $a=4\pm \sqrt {15}$．
圆心 $ \left(1,a\right)$ 到直线 $ax+y-2=0$ 的距离为 $\dfrac {\left|2a-2\right|}{\sqrt {a^2+1}}$，所以\[\dfrac {\left|2a-2\right|}{\sqrt {a^2+1}}=\sqrt 3,\]解得 $a=4\pm \sqrt {15}$．
题目
答案
解析
备注
