在三棱柱 $ABC-A_1B_1C_1$ 中，$\angle BAC=90^\circ$，其正视图和侧视图都是边长为 $1$ 的正方形，俯视图是直角边的长为 $1$ 的等腰直角三角形．设点 $M$，$N$，$P$ 分别是棱 $AB$，$BC$，$B_1C_1$ 的中点，则三棱锥 $P-A_1MN$ 的体积是 ．
【难度】
【出处】
2015年高考四川卷（文）
【标注】
【答案】
$\dfrac{1}{24}$
【解析】
先由三视图还原几何体，再根据锥体的体积公式求解即可．将三视图还原，如图所示：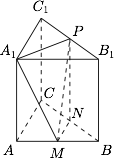
可得\[ V_{P-A_1MN}\overset {\left[a\right]}=V_{A_1-PMN}=\dfrac{1}{24}.\]（推导中用到 $\left[a\right]$．）
可得\[ V_{P-A_1MN}\overset {\left[a\right]}=V_{A_1-PMN}=\dfrac{1}{24}.\]（推导中用到 $\left[a\right]$．）
题目
答案
解析
备注
