已知函数 $f\left(x\right)=2^x$，$g\left(x\right)=x^2+ax$（其中 $a\in{\mathbb R}$）．对于不相等的实数 $x_1$，$x_2$，设 $m=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}$，$n=\dfrac{g\left(x_1\right)-g\left(x_2\right)}{x_1-x_2}$，现有如下命题：
① 对于任意不相等的实数 $x_1$，$x_2$，都有 $m>0$；
② 对于任意的 $a$ 及任意不相等的实数 $x_1$，$x_2$，都有 $n>0$；
③ 对于任意的 $a$，存在不相等的实数 $x_1$，$x_2$，使得 $m=n$；
④ 对于任意的 $a$，存在不相等的实数 $x_1$，$x_2$，使得 $m=-n$．
其中的真命题有 （写出所有真命题的序号）．
① 对于任意不相等的实数 $x_1$，$x_2$，都有 $m>0$；
② 对于任意的 $a$ 及任意不相等的实数 $x_1$，$x_2$，都有 $n>0$；
③ 对于任意的 $a$，存在不相等的实数 $x_1$，$x_2$，使得 $m=n$；
④ 对于任意的 $a$，存在不相等的实数 $x_1$，$x_2$，使得 $m=-n$．
其中的真命题有
【难度】
【出处】
无
【标注】
【答案】
①④
【解析】
题中 $m$ 与 $n$ 分别表示函数 $f\left(x\right)$ 与 $g\left(x\right)$ 图象上任意不同两点的斜率，很明显得出 ①② 的真假，对于 ③④ 可以通过 $m$ 与 $n$ 的关系把 $x_1$ 与 $x_2$ 分离，构造函数 $f\left(x\right)-g\left(x\right)$ 与 $f\left(x\right)+g\left(x\right)$ 后研究其性质得出真假结论．$m=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}$ 表示 $ f\left(x\right) $ 图象上两点 $ \left(x_1,f\left(x_1\right)\right)$ 和 $ \left(x_2,f\left(x_2\right)\right) $ 之间连线的斜率，$n=\dfrac{g\left(x_1\right)-g\left(x_2\right)}{x_1-x_2}$ 表示 $ g\left(x\right) $ 图象上两点 $ \left(x_1,g\left(x_1\right)\right)$ 和 $ \left(x_2,g\left(x_2\right)\right) $ 之间连线的斜率．
对于 ①：因为 $f\left(x\right)=2^x$在其定义域上单调递增，故 $ m>0 $，① 正确；
对于 ②：因为 $g\left(x\right)=x^2+ax$ 在其定义域上先减后增，所以存在 $ n<0 $ 的情况，② 错；
对于 ③：由 $ m=n $，得 $f\left(x_1\right)-f\left(x_2\right)=g\left(x_1\right)-g\left(x_2\right) $，即 $ f\left(x_1\right)-g\left(x_1\right)=f\left(x_2\right)-g\left(x_2\right) $．
令 $ h\left(x\right)=f\left(x\right)-g\left(x\right)=2^x-x^2-ax$，则 $ h'\left(x\right)=2^x\ln 2-2x-a $．令 $ h'\left(x\right)=0 $，得 $ 2^x \ln 2=2x+a$，如图：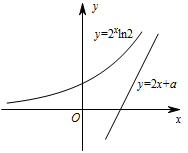
当 $ a $ 很小时，两图象无交点，且 $ 2^x\ln 2>2x+a $，故 $ h'\left(x\right)>0 $，$ h\left(x\right)$ 单调递增，此时不存在不相等的两个实数 $x_1 $，$x_2 $ 使得 $h\left(x_1\right)=h\left(x_2\right) $，即 $ f\left(x_1\right)-g\left(x_1\right)=f\left(x_2\right)-g\left(x_2\right) $ 成立，故 ③ 错；
对于 ④：由 $ m=-n $，得 $ f\left(x_1\right)+g\left(x_1\right)=f\left(x_2\right)+g\left(x_2\right) $．令 $ \varphi \left(x\right) =f\left(x\right)+g\left(x\right)=2^x+x^2+ax$，则 $ \varphi '\left(x\right)=2^x \ln 2+2x+a $．令 $ \varphi '\left(x\right)=0 $，得 $ 2^x\ln 2=-2x-a$，如图：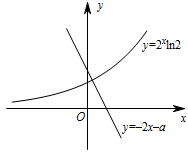
由图象知，$ y= 2^x\ln 2 $ 与 $y= -2x-a$ 图象必有交点，故 $ \varphi \left(x\right) $ 一定先减后增，所以一定存在不相等的两个实数 $ x_1 $，$ x_2 $ 使得 $ \varphi \left(x_1\right)=\varphi \left(x_2\right)$，即 $ f\left(x_1\right)+g\left(x_1\right)=f\left(x_2\right)+g\left(x_2\right) $ 成立，故 ④ 正确．
对于 ①：因为 $f\left(x\right)=2^x$在其定义域上单调递增，故 $ m>0 $，① 正确；
对于 ②：因为 $g\left(x\right)=x^2+ax$ 在其定义域上先减后增，所以存在 $ n<0 $ 的情况，② 错；
对于 ③：由 $ m=n $，得 $f\left(x_1\right)-f\left(x_2\right)=g\left(x_1\right)-g\left(x_2\right) $，即 $ f\left(x_1\right)-g\left(x_1\right)=f\left(x_2\right)-g\left(x_2\right) $．
令 $ h\left(x\right)=f\left(x\right)-g\left(x\right)=2^x-x^2-ax$，则 $ h'\left(x\right)=2^x\ln 2-2x-a $．令 $ h'\left(x\right)=0 $，得 $ 2^x \ln 2=2x+a$，如图：
当 $ a $ 很小时，两图象无交点，且 $ 2^x\ln 2>2x+a $，故 $ h'\left(x\right)>0 $，$ h\left(x\right)$ 单调递增，此时不存在不相等的两个实数 $x_1 $，$x_2 $ 使得 $h\left(x_1\right)=h\left(x_2\right) $，即 $ f\left(x_1\right)-g\left(x_1\right)=f\left(x_2\right)-g\left(x_2\right) $ 成立，故 ③ 错；对于 ④：由 $ m=-n $，得 $ f\left(x_1\right)+g\left(x_1\right)=f\left(x_2\right)+g\left(x_2\right) $．令 $ \varphi \left(x\right) =f\left(x\right)+g\left(x\right)=2^x+x^2+ax$，则 $ \varphi '\left(x\right)=2^x \ln 2+2x+a $．令 $ \varphi '\left(x\right)=0 $，得 $ 2^x\ln 2=-2x-a$，如图：
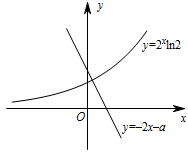由图象知，$ y= 2^x\ln 2 $ 与 $y= -2x-a$ 图象必有交点，故 $ \varphi \left(x\right) $ 一定先减后增，所以一定存在不相等的两个实数 $ x_1 $，$ x_2 $ 使得 $ \varphi \left(x_1\right)=\varphi \left(x_2\right)$，即 $ f\left(x_1\right)+g\left(x_1\right)=f\left(x_2\right)+g\left(x_2\right) $ 成立，故 ④ 正确．
题目
答案
解析
备注
