先用向量法表示出 $\cos \theta$，再换元表示 $\cos \theta$，最后利用二次函数的性质算出最值．因四边形 $ABCD$ 和 $ADPQ$ 均为正方形，且它们所在的平面互相垂直，故可以建立如图所示的空间直角坐标系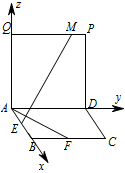：设正方形边长为 $2 $，则 $M\left(0,y,2\right) $（$ 0\leqslant y\leqslant2 $），$A\left(0,0,0\right) $，$E\left(1,0,0\right) $，$F\left(2,1,0\right) $，所以 $ \overrightarrow{EM}=\left(-1,y,2\right) $，$ \overrightarrow{AF}=\left(2,1,0\right) $，所以\[ \cos \theta \overset {\left[a\right]}=\left|\dfrac{\overrightarrow{EM}\cdot \overrightarrow{AF}}{\left|\overrightarrow{EM}\right|\cdot\left|\overrightarrow{AF}\right|}\right | =\dfrac{2-y}{\sqrt 5\cdot \sqrt{y^2+5}}.\]（推导中用到 $\left[a\right]$．）令 $t=2-y $，则 $0\leqslant t\leqslant 2 $．当 $t=0 $ 时，$ \cos \theta =0 $；当 $ 0<t\leqslant 2 $ 时，\[\begin{split}\cos \theta &=\dfrac {1}{\sqrt 5}\cdot \dfrac{t}{\sqrt{9-4t+t^2}}\\& =\dfrac{1}{\sqrt 5}\cdot \dfrac{1}{\sqrt {\left(\dfrac 3t -\dfrac 23\right)^2+\dfrac 59}} ,\end{split}\]因为 $ \dfrac 3t \geqslant \dfrac 32 $，所以当 $ \dfrac 3t =\dfrac 32$，即 $ t=2 $ 时，亦即点 $M$ 与点 $Q$ 重合时，$ \cos \theta $ 取最大值 $ \dfrac 25 $．