在平面直角坐标系 $xOy$ 中，若直线 $y=2a$ 与函数 $y= \left|x-a \right|-1$ 的图象只有一个交点，则 $a$ 的值为 ．
【难度】
【出处】
2015年高考安徽卷（文）
【标注】
【答案】
$-\dfrac12$
【解析】
由题意知，$2a$ 为函数 $y= \left|x-a \right|-1$ 的最小值，根据绝对值的意义，可得出函数 $f(x)= \left|x-a \right|-1$ 的最小值为 $f(a)$．函数 $f\left(x\right)= \left|x-a \right|-1$ 的图象如图所示，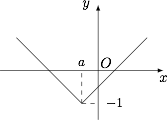
其最小值为 $ f\left(a\right)=-1 $．所以直线 $y=2a$ 与函数 $y= \left|x-a \right|-1$ 的图象只有一个交点时，有 $2a=-1$，解得 $a=-\dfrac 12$．
其最小值为 $ f\left(a\right)=-1 $．所以直线 $y=2a$ 与函数 $y= \left|x-a \right|-1$ 的图象只有一个交点时，有 $2a=-1$，解得 $a=-\dfrac 12$．
题目
答案
解析
备注
