设 ${P_1}$,${P_2}$,$ \cdots $,${P_n}$ 为平面 $\alpha $ 内的 $n$ 个点,在平面 $\alpha $ 内的所有点中,若点 $P$ 到 ${P_1}$,${P_2}$,$ \cdots $,${P_n}$ 点的距离之和最小,则称点 $P$ 为 ${P_1}$,${P_2}$,$ \cdots$,${P_n}$ 点的一个"中位点".例如,线段 $AB$ 上的任意点都是端点 $A$,$B$ 的中位点.则有下列命题:
① 若三个点 $A$,$B$,$C$ 共线,$C$ 在线段 $AB$ 上,则 $C$ 是 $A$,$B$,$C$ 的中位点;
② 直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③ 若四个点 $A$,$B$,$C$,$D$ 共线,则它们的中位点存在且唯一;
④ 梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是 .(写出所有真命题的序号)
① 若三个点 $A$,$B$,$C$ 共线,$C$ 在线段 $AB$ 上,则 $C$ 是 $A$,$B$,$C$ 的中位点;
② 直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③ 若四个点 $A$,$B$,$C$,$D$ 共线,则它们的中位点存在且唯一;
④ 梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是
【难度】
【出处】
2013年高考四川卷(理)
【标注】
【答案】
①④
【解析】
从两点之间线段最短这一结论入手思考,对于假命题只需要举出反例即可.显然 ① 是真命题.
考虑 ②:
如图(1),在 $\mathrm{Rt} \triangle ABC$ 中,$\angle C = 90^\circ $,$P$ 是 $AB$ 的中点,$CH \perp AB$,点 $P$,$H$ 不重合,则\[|PC| > |HC|.\]又 $|HA| + |HB| = |PA| + |PB| = |AB|$,所以\[|HA| + |HB| + |HC| \overset {\left[a\right]}< |PA| + |PB| + |PC|,\](推导中用到 $\left[a\right]$.)所以点 $P$ 不是点 $A$,$B$,$C$ 的中位点,故 ② 是假命题.
考虑 ③:
如图(2),$A$,$B$,$C$,$D$ 是数轴上的四个点,若 $P$ 点在线段 $BC$ 上,则\[|PA| + |PB| + |PC| + |PD| = |AD| + |BC|,\]又 $|PA| + |PB| + |PC| + |PD| \geqslant |AD| + |BC|$,故由中位点的定义及 ① 可知,点 $A$,$B$,$C$,$D$ 的中位点可能不唯一,故 ③ 是假命题.
如图(3),因为 $|PA| + |PB| + |PC| + |PD| \geqslant |AC| + |BD|$,等号成立当且仅当 $P$ 是 $AC$,$BD$ 的交点,所以梯形对角线的交点是梯形四个顶点的唯一中位点,故 ④ 是真命题.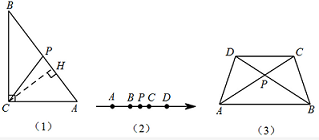
考虑 ②:
如图(1),在 $\mathrm{Rt} \triangle ABC$ 中,$\angle C = 90^\circ $,$P$ 是 $AB$ 的中点,$CH \perp AB$,点 $P$,$H$ 不重合,则\[|PC| > |HC|.\]又 $|HA| + |HB| = |PA| + |PB| = |AB|$,所以\[|HA| + |HB| + |HC| \overset {\left[a\right]}< |PA| + |PB| + |PC|,\](推导中用到 $\left[a\right]$.)所以点 $P$ 不是点 $A$,$B$,$C$ 的中位点,故 ② 是假命题.
考虑 ③:
如图(2),$A$,$B$,$C$,$D$ 是数轴上的四个点,若 $P$ 点在线段 $BC$ 上,则\[|PA| + |PB| + |PC| + |PD| = |AD| + |BC|,\]又 $|PA| + |PB| + |PC| + |PD| \geqslant |AD| + |BC|$,故由中位点的定义及 ① 可知,点 $A$,$B$,$C$,$D$ 的中位点可能不唯一,故 ③ 是假命题.
如图(3),因为 $|PA| + |PB| + |PC| + |PD| \geqslant |AC| + |BD|$,等号成立当且仅当 $P$ 是 $AC$,$BD$ 的交点,所以梯形对角线的交点是梯形四个顶点的唯一中位点,故 ④ 是真命题.

题目
答案
解析
备注