已知曲线 $C:x = - \sqrt {4 - {y^2}} $，直线 $l:x = 6$．若对于点 $A\left( {m,0} \right)$，存在 $C$ 上的点 $P$ 和 $l$ 上的 $Q$ 使得 $\overrightarrow {AP} + \overrightarrow {AQ} = \overrightarrow 0 $，则 $m$ 的取值范围为 ．
【难度】
【出处】
无
【标注】
【答案】
$\left[2,3\right]$
【解析】
曲线 $C$ 是以原点 $O$ 为圆心，$2$ 为半径的半圆．根据题意，由 $\overrightarrow{AP}+\overrightarrow{AQ}=\overrightarrow{0}$ 得 $A$ 是线段 $PQ$ 的中点．考虑当 $P,Q$ 运动时，其中点 $M$ 构成的平面区域：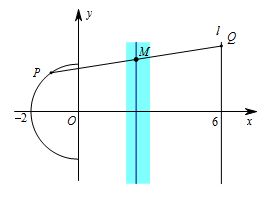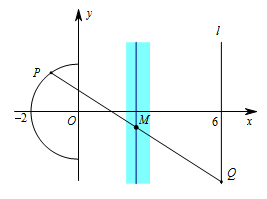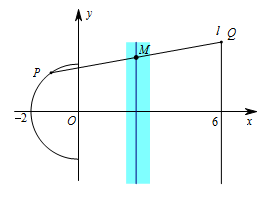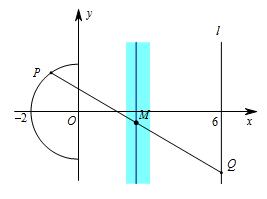
先固定 $P$ 点为 $\left(x_P,y_P\right)$，让 $Q$ 点在直线 $l$ 上运动，这样就得到对应的 $M$ 点的轨迹是一条竖直的直线 $x=\dfrac{x_P+6}2$．然后让 $P$ 点在半圆上运动，则 $M$ 点的轨迹随之运动形成的区域即所有满足条件的 $M$ 点的集合，如图．因此 $m$ 的取值范围是 $\left[\dfrac{-2+6}2,\dfrac{0+6}2\right]$，即 $\left[2,3\right]$．
先固定 $P$ 点为 $\left(x_P,y_P\right)$，让 $Q$ 点在直线 $l$ 上运动，这样就得到对应的 $M$ 点的轨迹是一条竖直的直线 $x=\dfrac{x_P+6}2$．然后让 $P$ 点在半圆上运动，则 $M$ 点的轨迹随之运动形成的区域即所有满足条件的 $M$ 点的集合，如图．因此 $m$ 的取值范围是 $\left[\dfrac{-2+6}2,\dfrac{0+6}2\right]$，即 $\left[2,3\right]$．
题目
答案
解析
备注
