直线 ${l_1}$ 和 ${l_2}$ 是圆 ${x^2} + {y^2} = 2$ 的两条切线,若 ${l_1}$ 与 ${l_2}$ 的交点为 $\left( {1,3} \right)$,则 ${l_1}$ 与 ${l_2}$ 的夹角的正切值等于 .
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{4}{3}$
【解析】
先在直角三角形中利用斜边和直角边求出切线与 $OA$ 的夹角,再利用二倍角公式求出两条切线的夹角.设 $l_1$,$l_2$ 与圆分别切于 $ B$、$C$ 两点,如图所示,则 $ OB\perp AB$.$ |OB|=\sqrt 2$,$|OA|=\sqrt {\left(1-0\right)^2+\left(3-0\right)^2}=\sqrt {10}$,从而 $ |AB|=2\sqrt 2$.设 $ \angle OAB=\theta$,则 $ \tan \theta=\dfrac 12$,所以 $ \tan \angle CAB=\tan 2\theta=\dfrac {2\tan \theta}{1-\tan ^2\theta}=\dfrac{4}{3}$.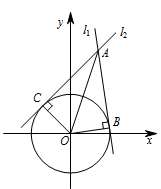

题目
答案
解析
备注