某高科技企业生产产品 $A$ 和产品 $B$ 需要甲、乙两种新型材料．生产一件产品 $A$ 需要甲材料 $1.5\mathrm{kg}$，乙材料 $1\mathrm{kg}$，用 $5$ 个工时；生产一件产品 $B$ 需要甲材料 $0.5\mathrm{kg}$，乙材料 $0.3\mathrm{kg}$，用 $3$ 个工时．生产一件产品 $A$ 的利润为 $2100$ 元，生产一件产品 $B$ 的利润为 $900$ 元．该企业现有甲材料 $150\mathrm{kg}$，乙材料 $90\mathrm{kg}$，则在不超过 $600$ 个工时的条件下，生产产品 $A$、产品 $B$ 的利润之和的最大值为 元．
【难度】
【出处】
无
【标注】
【答案】
$216000$
【解析】
根据题中条件列出约束条件，写出目标函数，作出可行域进行求解即可，注意到这里的变量均为正整数．设生产产品 $A,B$ 的件数分别为 $x,y$ 时，获得利润为 $z$ 元．则 $x,y$ 满足的约束条件为\[\begin{cases} 1.5x+0.5y\leqslant 150,\\x+0.3y\leqslant 90,\\5x+3y\leqslant 600,\end{cases}\]其中 $x,y\in \mathbb{N}^*$，目标函数 $z=2100x+900y=300\left(7x+3y\right)$．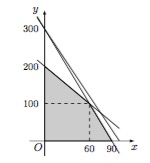
作出可行域，可以得到当 $x=60,y=100$ 时，$z$ 有最大值 $216000$．
作出可行域，可以得到当 $x=60,y=100$ 时，$z$ 有最大值 $216000$．
题目
答案
解析
备注
