在平面直角坐标系中，当 $P\left(x,y\right)$ 不是原点时，定义 $P$ 的“伴随点”为 $P'\left(\dfrac{y}{x^2+y^2},\dfrac{-x}{x^2+y^2}\right)$；
当 $P$ 是原点时，定义 $P$ 的“伴随点“为它自身，平面曲线 $C$ 上所有点的“伴随点”所构成的曲线 $C'$ 定义为曲线 $C$ 的“伴随曲线”．现有下列命题：
① 若点 $A$ 的“伴随点”是点 $A'$，则点 $A'$ 的“伴随点”是点 $A$；
② 单位圆的“伴随曲线”是它自身；
③ 若曲线 $C$ 关于 $x$ 轴对称，则其“伴随曲线”$C'$ 关于 $y$ 轴对称；
④ 一条直线的“伴随曲线”是一条直线．
其中的真命题是 （写出所有真命题的序号）．
当 $P$ 是原点时，定义 $P$ 的“伴随点“为它自身，平面曲线 $C$ 上所有点的“伴随点”所构成的曲线 $C'$ 定义为曲线 $C$ 的“伴随曲线”．现有下列命题：
① 若点 $A$ 的“伴随点”是点 $A'$，则点 $A'$ 的“伴随点”是点 $A$；
② 单位圆的“伴随曲线”是它自身；
③ 若曲线 $C$ 关于 $x$ 轴对称，则其“伴随曲线”$C'$ 关于 $y$ 轴对称；
④ 一条直线的“伴随曲线”是一条直线．
其中的真命题是
【难度】
【出处】
无
【标注】
【答案】
②③
【解析】
本题考查对新知识的理解转化能力，主要根据题中伴随点的坐标变换形式，联系到极坐标是解决本题的关键．观察伴随点的坐标形式，考虑利用极坐标理解“伴随点”．设 $P\left(\rho\cos\theta,\rho\sin\theta\right)$，其中 $\rho>0$，则其伴随点 $P'$ 为 $\left(\dfrac{1}{\rho}\sin\theta,-\dfrac{1}{\rho}\cos\theta\right)$，即 $\left(\dfrac{1}{\rho}\cos\left(\theta-\dfrac{\mathrm \pi} 2\right),\dfrac{1}{\rho}\sin\left(\theta-\dfrac{\mathrm \pi} 2\right)\right)$．可以理解为将 $P$ 绕 $O$ 顺时针旋转 $\dfrac{\mathrm \pi} 2$ 得到点 $Q$，然后在射线 $OQ$ 上取 $P'$ 使得 $|OP'|=\dfrac{1}{\rho}$（可以看成关于单位圆反演），如图．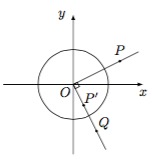
对命题 ①，取单位圆上的一点 $A$，那么它的“伴随点”$A'$ 的“伴随点”相当于将 $A$ 顺时针旋转 ${\mathrm \pi} $ 得到的点，与点 $A$ 关于原点对称，命题错误；
对命题 ②，根据对“伴随点”的几何解释，命题正确；
对命题 ③，若曲线 $C$ 关于 $x$ 轴对称，那么曲线 $C$ 顺时针旋转 $\dfrac{\mathrm \pi} 2$ 后得到的曲线 $D$ 必然关于 $y$ 轴对称，此时将曲线 $D$ 关于单位圆反演得到的曲线必然也关于 $y$ 轴对称，命题正确；
对命题 ④，任取与单位圆相离的直线，则其“伴随曲线”必然在单位圆内部，不可能是一条直线，命题错误．
综上所述，真命题是 ②③．
对命题 ①，取单位圆上的一点 $A$，那么它的“伴随点”$A'$ 的“伴随点”相当于将 $A$ 顺时针旋转 ${\mathrm \pi} $ 得到的点，与点 $A$ 关于原点对称，命题错误；对命题 ②，根据对“伴随点”的几何解释，命题正确；
对命题 ③，若曲线 $C$ 关于 $x$ 轴对称，那么曲线 $C$ 顺时针旋转 $\dfrac{\mathrm \pi} 2$ 后得到的曲线 $D$ 必然关于 $y$ 轴对称，此时将曲线 $D$ 关于单位圆反演得到的曲线必然也关于 $y$ 轴对称，命题正确；
对命题 ④，任取与单位圆相离的直线，则其“伴随曲线”必然在单位圆内部，不可能是一条直线，命题错误．
综上所述，真命题是 ②③．
题目
答案
解析
备注
