先根据分段函数的单调性得到 $a$ 的取值范围，再从得到的范围上分析所给方程有两个不同实数解的条件求出最终的 $a$ 的范围．因为 $ f\left(x\right) $ 在 $ \mathbb {R} $ 上单调递减，所以\[ \begin{cases} -\dfrac{4a-3}{2}\geqslant 0,\\ 0<a<1,\\ \left.\left[{x}^{2}+\left(4a-3\right)x+3a\right]\right|_{x=0} \geqslant \left.\left[{{\log }_{a}}\left(x+1\right)+1\right]\right|_{x=0}, \end{cases}\]解得 $\dfrac{1}{3}\leqslant a \leqslant \dfrac{3}{4}$．
接下来思考函数 $ y=f\left(x\right) $ 的图象与射线 $ y=2-\dfrac x3 $（$ x\leqslant 6 $）以及 $ y=\dfrac x3-2 $（$ x\leqslant 6 $）的公共点个数，如图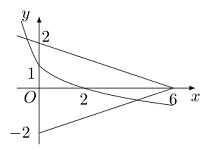．当 $ a=\dfrac 13 $ 时，符合题意．当 $ a $ 变大时，设函数 $ h\left(x\right)={\log_a}\left(x+1\right)+1 $（$ x\geqslant 0 $），则 $ h\left(0\right)=1 $，而 $ h\left(2\right)={\log_a}3+1<0 $，因此在区间 $ \left[0,6\right] $ 上题中方程有且只有一个实数解．
这样问题就转化为了方程\[ x^2+\left(4a-3\right)x+3a=2-\dfrac x3 \]在区间 $ \left(-\infty,0\right) $ 上只有一个实数解．
设 $ g\left(x\right)=x^2+4\left(a-\dfrac 23\right)x+3a-2 $，则 $ g\left(0\right)=3a-2 $，因此得到分界点 $ \dfrac 23 $．
情形一：$ \dfrac 13\leqslant a<\dfrac 23 $．
此时 $ g\left(0\right)<0 $，而 $ g\left(x\right) $ 的图象开口向上，因此方程在区间 $ \left(-\infty,0\right) $ 上有且只有一个实数解，符合题意．
情形二：$ a=\dfrac 23 $．
此时 $ g\left(0\right)=0 $，而 $ g\left(x\right) $ 的对称轴为 $ x=0 $，于是方程在区间 $ \left(-\infty,0\right) $ 上没有实数解，不符合题意．
情形三：$ \dfrac 23<a\leqslant \dfrac 34 $．
此时 $ g\left(0\right)>0 $，而 $ g\left(x\right) $ 的对称轴 $ x=-2\left(a-\dfrac 23\right) $ 满足 $ -2\left(a-\dfrac 23\right)<0 $，进一步可得其判别式\[ \Delta=16\left(a-\dfrac 23\right)^2-12\left(a-\dfrac 23\right)<0, \]于是方程在区间 $ \left(-\infty,0\right) $ 上没有实数解，不符合题意．
综上所述，$ a $ 的取值范围是 $ \left[\dfrac 13,\dfrac 23\right) $．