设抛物线 $\begin{cases}
x=2p{{t}^{2}} ,\\
y=2pt \\
\end{cases} $（$t$ 为参数，$p>0$）的焦点为 $F$，准线为 $l$．过抛物线上一点 $A$ 作 $l$ 的垂线，垂足为 $B$．设 $C\left(\dfrac{7}{2} p,0\right)$，$AF$ 与 $BC$ 相交于点 $E$．若 $|CF|=2|AF|$，且 $\triangle ACE$ 的面积为 $3\sqrt{2}$，则 $p$ 的值为 ．
x=2p{{t}^{2}} ,\\
y=2pt \\
\end{cases} $（$t$ 为参数，$p>0$）的焦点为 $F$，准线为 $l$．过抛物线上一点 $A$ 作 $l$ 的垂线，垂足为 $B$．设 $C\left(\dfrac{7}{2} p,0\right)$，$AF$ 与 $BC$ 相交于点 $E$．若 $|CF|=2|AF|$，且 $\triangle ACE$ 的面积为 $3\sqrt{2}$，则 $p$ 的值为
【难度】
【出处】
无
【标注】
【答案】
$\sqrt 6$．
【解析】
先根据抛物线的定义，得 $ AB=AF $，再利用相似三角形的性质解答即可．由题意可知，抛物线的普通方程为 $ y^2=2px\left(p>0\right) $，$ F $ 点坐标为 $ \left(\dfrac{p}{2},0 \right) $，准线 $ l $ 的方程为 $ x=-\dfrac{p}{2} $，如图．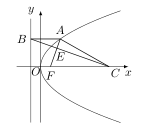
设 $ A $ 点坐标为 $ \left(x_1,y_1\right) $，不妨设 $ y_1>0 $．由于 $ \left|CF\right|=2\left|AF\right| $，故\[ 2\left(x_1+\dfrac{p}{2} \right)=3p, 解得 x_1=p, \]进一步可求得 $ A $ 点坐标为 $ \left(p,\sqrt{2}p\right) $．
因为 $ \triangle{ABE} $ 与 $ \triangle{FCE} $ 相似，且 $ \dfrac{\left|AB\right|}{\left|FC\right|}=\dfrac{1}{2} $，所以\[ S_{\triangle{ACF}}=3S_{\triangle{ACE}}=9\sqrt{2}, 即 \dfrac{1}{2}\cdot 3p \cdot \sqrt{2}p=9\sqrt{2}, \]解得 $ p=\sqrt{6} $．
设 $ A $ 点坐标为 $ \left(x_1,y_1\right) $，不妨设 $ y_1>0 $．由于 $ \left|CF\right|=2\left|AF\right| $，故\[ 2\left(x_1+\dfrac{p}{2} \right)=3p, 解得 x_1=p, \]进一步可求得 $ A $ 点坐标为 $ \left(p,\sqrt{2}p\right) $．因为 $ \triangle{ABE} $ 与 $ \triangle{FCE} $ 相似，且 $ \dfrac{\left|AB\right|}{\left|FC\right|}=\dfrac{1}{2} $，所以\[ S_{\triangle{ACF}}=3S_{\triangle{ACE}}=9\sqrt{2}, 即 \dfrac{1}{2}\cdot 3p \cdot \sqrt{2}p=9\sqrt{2}, \]解得 $ p=\sqrt{6} $．
题目
答案
解析
备注
