设双曲线 $x^2-\dfrac{y^2}3=1$ 的左、右焦点分别为 $F_1,F_2$．若点 $P$ 在双曲线上，且 $\triangle F_1PF_2$ 为锐角三角形，则 $|PF_1|+|PF_2|$ 的取值范围是 ．
【难度】
【出处】
2016年高考浙江卷（文）
【标注】
【答案】
$\left(2\sqrt 7,8\right)$
【解析】
本题可以先考虑直角三角形的情况，然后再考虑锐角三角形的情况．不妨设 $P$ 在第一象限，如图所示：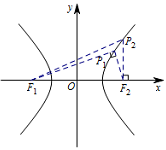
当 $P$ 位于 $P_2$ 点时 $\angle F_1F_2P=90^\circ,$ 此时有\[\begin{cases}|PF_1|-|PF_2|=2,\\|PF_1|^2=|PF_2|^2+4^2.\end{cases}\]可得到\[|PF_1|+|PF_2|=8.\]当 $P$ 位于 $P_1$ 点时 $\angle F_1PF_2=90^\circ,$ 此时有\[\begin{cases}|PF_1|-|PF_2|=2,\\|PF_1|^2+|PF_2|^2=4^2.\end{cases}\]可得到\[|PF_1|+|PF_2|=2\sqrt 7.\]分析可知，点 $P$ 位于 $P_1$ 与 $P_2$ 之间，所以 $|PF_1|+|PF_2|$ 的取值范围是 $\left(2\sqrt 7,8\right)$．
当 $P$ 位于 $P_2$ 点时 $\angle F_1F_2P=90^\circ,$ 此时有\[\begin{cases}|PF_1|-|PF_2|=2,\\|PF_1|^2=|PF_2|^2+4^2.\end{cases}\]可得到\[|PF_1|+|PF_2|=8.\]当 $P$ 位于 $P_1$ 点时 $\angle F_1PF_2=90^\circ,$ 此时有\[\begin{cases}|PF_1|-|PF_2|=2,\\|PF_1|^2+|PF_2|^2=4^2.\end{cases}\]可得到\[|PF_1|+|PF_2|=2\sqrt 7.\]分析可知，点 $P$ 位于 $P_1$ 与 $P_2$ 之间，所以 $|PF_1|+|PF_2|$ 的取值范围是 $\left(2\sqrt 7,8\right)$．
题目
答案
解析
备注
