本题可以考虑利用向量求解，注意到三角形 $ABC$ 和三角形 $ACD$ 中的线段的相对位置关系不发生改变，可以把 $\overrightarrow{BD'}$ 分解为 $\overrightarrow{BO}$ 与 $\overrightarrow{OD'}$ 的和（$O$ 为 $AC$ 中点），于是 $\overrightarrow{BD'}\cdot\overrightarrow{AC}$ 和 $|\overrightarrow{AC}|$ 为定值，只要考虑 $|\overrightarrow{BD'}|$ 的变化即可．找到线段 $AC$ 的中点 $O$，连接 $OB$、$OD$、$OD'$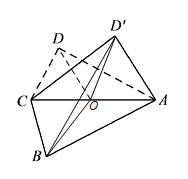，显然有\[\overrightarrow{BD'}=\overrightarrow{BO}+\overrightarrow{OD'},\]于是\[ \begin{split}\overrightarrow{BD'}\cdot\overrightarrow{AC}&=\overrightarrow{OD'}\cdot\overrightarrow{AC}+\overrightarrow {BO}\cdot \overrightarrow {AC}\\&=\overrightarrow{OD'}\cdot\overrightarrow{AC}\\&=2,\end{split} \]为定值，设直线 $AC$ 与 $BD'$ 所成的角为 $\theta$，则有\[\cos \theta=\left|\dfrac{\overrightarrow{BD'}\cdot\overrightarrow{AC}}{\left|\overrightarrow{BD'}\right|\cdot\left|\overrightarrow{AC}\right|}\right|=\dfrac 2{\sqrt 6 \left|\overrightarrow{BD'}\right|}.\]于是 $\cos \theta$ 的值取决于 $\left|\overrightarrow{BD'}\right|$ 的大小．
当 $D'$ 位于 $D_1$ 的位置时（$A$、$B$、$C$、$D'$ 在一个平面内，且 $D'$ 与 $B$ 位于 $AC$ 异侧），$BD'$ 最大，为 $\sqrt {14}$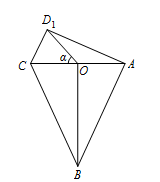；当 $D'$ 位于 $D_2$ 的位置时（$A$、$B$、$C$、$D'$ 在一个平面内，且 $D'$ 与 $B$ 位于 $AC$ 同侧），$BD'$ 最小，为 $2$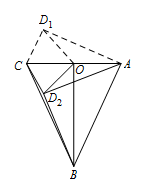．因此 $\cos \theta$ 的最大值为 $\dfrac{\sqrt 6}6$；最小值为 $\dfrac{\sqrt{21}}{21}$．