已知三棱锥 $S-ABC$ 的所有顶点都在球 $O$ 的球面上，$SC$ 是球 $O$ 的直径．若平面 $SCA\perp$ 平面 $SCB$，$SA=AC$，$SB=BC$，三棱锥 $S-ABC$ 的体积为 $9$，则球 $O$ 的表面积为 ．
【难度】
【出处】
2017年高考全国乙卷（文）
【标注】
【答案】
$36\pi$
【解析】
如图，连接 $OA,OB$．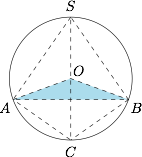
根据题意，三角形 $SAC,SBC$ 均为等腰直角三角形，而 $O$ 为斜边 $SC$ 的中点，因此 $OA,OB,OS$ 两两垂直．设球 $O$ 的半径为 $r$，则三棱锥$S-ABC$ 的体积\[V=\dfrac 13\cdot S_{\triangle OAB}\cdot SC=\dfrac 13\cdot \dfrac 12r^2\cdot 2r=\dfrac 13r^3=9,\]解得 $r=3$，因此球$O$ 的表面积 $S=4\pi r^2=36 \pi $．
根据题意，三角形 $SAC,SBC$ 均为等腰直角三角形，而 $O$ 为斜边 $SC$ 的中点，因此 $OA,OB,OS$ 两两垂直．设球 $O$ 的半径为 $r$，则三棱锥$S-ABC$ 的体积\[V=\dfrac 13\cdot S_{\triangle OAB}\cdot SC=\dfrac 13\cdot \dfrac 12r^2\cdot 2r=\dfrac 13r^3=9,\]解得 $r=3$，因此球$O$ 的表面积 $S=4\pi r^2=36 \pi $．
题目
答案
解析
备注
