如图是抛物线形拱桥，当水面在 $ l $ 时，拱顶离水面 $ 2 $ 米，水面宽 $ 4 $ 米．水位下降 $ 1 $ 米后，水面宽 米．
【难度】
【出处】
无
【标注】
【答案】
$ 2{\sqrt{6}} $
【解析】
建立合适的坐标系并求出抛物线方程，然后求解．以拱顶为原点建立直角坐标系，如图所示：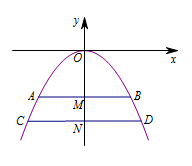
设抛物线的方程为 $x^2=2py$，把点 $B\left(2,-2\right)$ 代入可求得 $p=-1$，也即抛物线方程为\[x^2=-2y.\]显然\[|MN|=1.\]设 $D\left(x_0,-3\right)$，代入抛物线方程可得\[x_0=\sqrt 6.\]所以此时的水面宽为 $2x_0=2\sqrt 6$ 米．
设抛物线的方程为 $x^2=2py$，把点 $B\left(2,-2\right)$ 代入可求得 $p=-1$，也即抛物线方程为\[x^2=-2y.\]显然\[|MN|=1.\]设 $D\left(x_0,-3\right)$，代入抛物线方程可得\[x_0=\sqrt 6.\]所以此时的水面宽为 $2x_0=2\sqrt 6$ 米．
题目
答案
解析
备注
