如图，在正方体 $ ABCD-A_1B_1C_1D_1 $ 中，$ M、N $ 分别是棱 $ CD、CC_1 $ 的中点，则异面直线 $ A_1M $ 与 $ DN $ 所成的角的大小是 ．
【难度】
【出处】
无
【标注】
【答案】
$ 90^\circ $
【解析】
本题通过证明两条异面直线垂直得到其所成角是 $90^{\circ}$．如图，连接 $ D_1M $，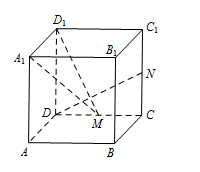
则 $ DN\perp D_1M$，又 $ DN\perp A_1D_1 $，所以 $ DN\perp 平面 A_1D_1M$，从而得到 $ A_1M\perp DN $，即直线 $ A_1M $ 与 $ DN $ 所成的角是 $ 90^\circ $．
则 $ DN\perp D_1M$，又 $ DN\perp A_1D_1 $，所以 $ DN\perp 平面 A_1D_1M$，从而得到 $ A_1M\perp DN $，即直线 $ A_1M $ 与 $ DN $ 所成的角是 $ 90^\circ $．
题目
答案
解析
备注
