设 $z = kx + y$，其中实数 $x$，$y$ 满足 ${\begin{cases}
x \geqslant 2, \\
x - 2y + 4 \geqslant 0, \\
2x - y - 4 \leqslant 0, \\
\end{cases}}$ 若 $z$ 的最大值为 $ 12 $，则实数 $k = $ ．
x \geqslant 2, \\
x - 2y + 4 \geqslant 0, \\
2x - y - 4 \leqslant 0, \\
\end{cases}}$ 若 $z$ 的最大值为 $ 12 $，则实数 $k = $
【难度】
【出处】
2013年高考浙江卷（文）
【标注】
【答案】
$ 2 $
【解析】
本题是一道线性规划问题，画出可行域，注意考虑 $k$ 的正负．画出可行域，如图所示，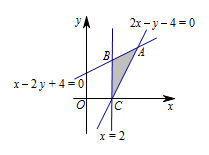
$z = kx + y$ 即 $y=-kx+z$，若 $k\geqslant 0$，则直线 $y=-kx+z$ 经过点 $A\left(4,4\right)$ 时，$z$ 取得最大值，即\[4=-4k+12,\]解得\[k=2.\]若 $k<0$，由于 $z$ 的最大值只可能在边界点取到，而 $A,B,C$ 三点的坐标代入 $12=kx+y$，得到的 $k$ 都为正数，所以不满足题意．
因此 $k=2$．
$z = kx + y$ 即 $y=-kx+z$，若 $k\geqslant 0$，则直线 $y=-kx+z$ 经过点 $A\left(4,4\right)$ 时，$z$ 取得最大值，即\[4=-4k+12,\]解得\[k=2.\]若 $k<0$，由于 $z$ 的最大值只可能在边界点取到，而 $A,B,C$ 三点的坐标代入 $12=kx+y$，得到的 $k$ 都为正数，所以不满足题意．因此 $k=2$．
题目
答案
解析
备注
