如图，$AB$ 是圆的直径，弦 $CD$ 与 $AB$ 相交于点 $E$，$BE=2AE=2$，$BD=ED$，则线段 $CE$ 的长为 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac {2}{3}\sqrt 3$．
【解析】
取 $BE$ 的中点为 $F$，连接 $DF$．利用射影定理或圆幂定理可求出 $DF$，进而得 $DE$，最后利用圆幂定理可求得 $CE$．作辅助线 $DF$ 是解答本题的关键．如图，取 $BE$ 的中点为 $F$，连接 $DF$．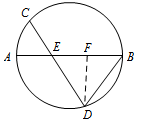
因为 $BD=ED$，$F$ 为 $BE$ 的中点，所以 $DF \perp BE$．所以\[DF^2\overset{\left[a\right]}=AF\cdot BF,\]（推导中用到 [a]）又因为 $BE=2AE=2$，所以 $DF=\sqrt 2$．
又因为\[DF^2+EF^2=DE^2,\]所以 $DE=\sqrt 3$．
又因为\[AE \cdot BE\overset{\left[b\right]}=CE \cdot DE,\]（推导中用到 [b]）所以解得 $CE=\dfrac {2}{3}\sqrt 3$．
因为 $BD=ED$，$F$ 为 $BE$ 的中点，所以 $DF \perp BE$．所以\[DF^2\overset{\left[a\right]}=AF\cdot BF,\]（推导中用到 [a]）又因为 $BE=2AE=2$，所以 $DF=\sqrt 2$．又因为\[DF^2+EF^2=DE^2,\]所以 $DE=\sqrt 3$．
又因为\[AE \cdot BE\overset{\left[b\right]}=CE \cdot DE,\]（推导中用到 [b]）所以解得 $CE=\dfrac {2}{3}\sqrt 3$．
题目
答案
解析
备注
