已知函数 $f\left(x\right)=\begin{cases}|x|,&x\leqslant m\\ x^{2}-2mx+4m,&x>m\end{cases}$ 其中 $m>0$,若存在实数 $b$,使得关于 $x$ 的方程 $f\left(x\right)=b$ 有三个不同的根,则 $m$ 的取值范围是 .
【难度】
【出处】
无
【标注】
【答案】
$ \left(3,+\infty\right) $
【解析】
本小题考查方程的根,借助于函数图象数形结合能够更快速解决此题.注意到函数 $ y=x^2-2mx+4m $($ x>m $)是在 $ \left(m,+\infty\right) $ 上的单调递增函数,因此若存在实数 $ b $,使得关于 $ x $ 的方程 $ f\left(x\right)=b $ 有三个不同的根,那么必然有\[\left.\left(|x|\right)\right|_{x=m}>\left.\left(x^2-2mx+4m\right)\right|_{x=m},\]解得 $ m>3 $,因此 $ m $ 的取值范围是 $ \left(3,+\infty\right) $.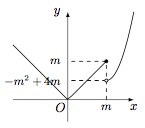

题目
答案
解析
备注