如图，将一张边长为 $1$ 的正方形纸 $ABCD$ 折叠，使得点 $B$ 始终落在边 $AD$ 上，则折叠的过程中线段 $EF$ 划过的面积为 ．
【难度】
【出处】
无
【标注】
【答案】
$ \dfrac{7}{24} $
【解析】
如图，作 $B'K\perp BC$ 于 $K$，连接 $BK$．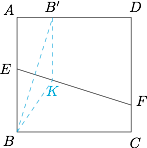
不难得到 $EF$ 始终与以 $B$ 为焦点，直线 $AD$ 为准线的抛物线相切于点 $K$（因为 $EF$ 上有且仅有一点在抛物线上）．这样我们就可以得到线段 $EF$ 关于点 $B'$ 形成的轨迹，如图所示．
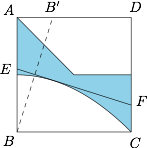由此，可以求得所求面积为$$1-\dfrac 38-\int_0^1{\left(\dfrac 12-\dfrac 12x^2\right)}{\mathrm d}x=\dfrac{7}{24}.$$
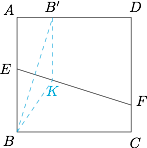不难得到 $EF$ 始终与以 $B$ 为焦点，直线 $AD$ 为准线的抛物线相切于点 $K$（因为 $EF$ 上有且仅有一点在抛物线上）．这样我们就可以得到线段 $EF$ 关于点 $B'$ 形成的轨迹，如图所示．由此，可以求得所求面积为$$1-\dfrac 38-\int_0^1{\left(\dfrac 12-\dfrac 12x^2\right)}{\mathrm d}x=\dfrac{7}{24}.$$
题目
答案
解析
备注
