查看数据源：5909955938b6b4000adaa286
设函数 $f(x)=\begin{cases}2^x-a,&x<1,\\4(x-a)(x-2a),&x\geqslant 1.\end{cases}$．
① 若 $a=1$，则 $f(x)$ 的最小值为 ；
② 若 $f(x)$ 恰有 $2$ 个零点，则实数 $a$ 的取值范围是 ．
【难度】
【出处】
2015年高考北京卷（理）
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    二次函数
  • 知识点
    >
    函数
    >
    分段函数
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的零点
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的最值和值域
【答案】
① $ -1$；② $\left[\dfrac 12,1\right)\cup\left[2,+\infty\right)$
【解析】
① 当 $a=1$ 时，函数 $f(x)$ 的图象如图，最小值为 $-1$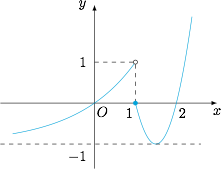．② 分段考虑函数 $f(x)$ 的零点．
直线 $x=1$ 左侧 $y=2^x-a$ 单调递增，且在 $x<1$ 时取值范围为 $(-a,2-a)$，于是只有当 $0<a<2$ 时函数 $f(x)$ 在直线 $x=1$ 左侧存在零点．
直线 $x=1$ 右侧（含 $x=1$）考虑 $y=4(x-a)(x-2a)$ 的两个零点 $x=a$ 和 $x=2a$，分别与 $x=1$ 进行比较，划分区间讨论，可得函数 $f(x)$ 在 $x\geqslant 1$ 时的零点个数为$$\begin{cases}0,&2a<1,\\1,&a<1\leqslant 2a,\\2,&1\leqslant a.\end{cases}$$综合以上，可得函数 $f(x)$ 恰有两个零点时，$a$ 的取值范围是 $\left[\dfrac 12,1\right)\cup\left[2,+\infty\right)$．
题目 答案 解析 备注
0.109858s