在平面四边形 $ABCD$ 中，$\angle A=\angle B=\angle C=75^\circ$，$BC=2$，则 $AB$ 的取值范围是 ．
【难度】
【出处】
2015年高考全国Ⅰ卷（理）
【标注】
【答案】
$\left(\sqrt 6-\sqrt 2,\sqrt 6 + \sqrt 2\right)$
【解析】
先设法作出符合题意的图形．
第一步 作两底角为 $75^\circ$，且底边长为 $2$ 的等腰三角形 $EBC$；
第二步 在边 $BE$ 上取点 $F$，使 $\angle BFC=75^\circ$，连接 $FC$；
第三步 在线段 $FE$ 上（不包含端点）任取一点为 $A$，过 $A$ 作 $FC$ 的平行线，交 $CE$ 于 $D$，如图．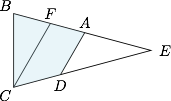
这样就有 $AB$ 的取值范围是线段 $BF$ 的长度到线段 $BE$ 的长度的开区间．
接下来计算 $BF$ 与 $BE$ 的长度．在 $\triangle BCF$ 中，易得$$BF=4\sin 15^\circ=4\sin (45^\circ-30^\circ)=\sqrt 6-\sqrt 2.$$而由于三角形 $BCF$ 和三角形 $BEC$ 相似，于是$$BE=\dfrac{BC^2}{BF}=\sqrt 6+\sqrt 2.$$
这样就有 $AB$ 的取值范围是线段 $BF$ 的长度到线段 $BE$ 的长度的开区间．接下来计算 $BF$ 与 $BE$ 的长度．在 $\triangle BCF$ 中，易得$$BF=4\sin 15^\circ=4\sin (45^\circ-30^\circ)=\sqrt 6-\sqrt 2.$$而由于三角形 $BCF$ 和三角形 $BEC$ 相似，于是$$BE=\dfrac{BC^2}{BF}=\sqrt 6+\sqrt 2.$$
题目
答案
解析
备注
