如图，已知正方形 $ABCD$ 的边长为 $2$，点 $E$ 为 $AB$ 的中点．以 $A$ 为圆心，$AE$ 为半径，作弧交 $AD$ 于点 $F$．若 $P$ 为劣弧 $EF$ 上的动点，则 $\overrightarrow{PC}\cdot\overrightarrow{PD}$ 的最小值为 ．
【难度】
【出处】
无
【标注】
【答案】
$5-2\sqrt 5$
【解析】
以 $A$ 为原点，$AB$ 为 $x$ 轴方向，$AD$ 为 $y$ 轴方向建立平面直角坐标系，如图．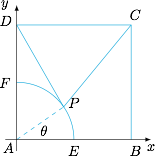
设 $\angle PAE=\theta$，则 $C(2,2)$、$D(0,2)$、$P\left(\cos\theta,\sin\theta\right)$，其中 $\theta\in\left[0,\dfrac{\pi}{2}\right]$．于是\[\begin{split}\overrightarrow{PC}\cdot\overrightarrow{PD}&=\left(2-\cos\theta,2-\sin\theta\right)\cdot\left(-\cos\theta,2-\sin\theta\right)\\&=5-4\sin\theta-2\cos\theta\\&=5-2\sqrt 5\sin\left(\theta+\varphi\right)\\&\geqslant 5-2\sqrt 5,\end{split}\]其中 $\varphi$ 为辅助角，且为锐角，等号可以取得．因此所求最小值为 $5-2\sqrt 5$．
设 $\angle PAE=\theta$，则 $C(2,2)$、$D(0,2)$、$P\left(\cos\theta,\sin\theta\right)$，其中 $\theta\in\left[0,\dfrac{\pi}{2}\right]$．于是\[\begin{split}\overrightarrow{PC}\cdot\overrightarrow{PD}&=\left(2-\cos\theta,2-\sin\theta\right)\cdot\left(-\cos\theta,2-\sin\theta\right)\\&=5-4\sin\theta-2\cos\theta\\&=5-2\sqrt 5\sin\left(\theta+\varphi\right)\\&\geqslant 5-2\sqrt 5,\end{split}\]其中 $\varphi$ 为辅助角，且为锐角，等号可以取得．因此所求最小值为 $5-2\sqrt 5$．
题目
答案
解析
备注
