过点 $M(4,3)$ 的动直线 $l$ 交 $x$ 轴的正半轴于点 $A$，交 $y$ 轴的正半轴于点 $B$．设点 $P$ 是三角形 $OAB$ 的面积取最小值时，三角形 $OAB$ 内切圆上的动点，则 $z=PO^2+PA^2+PB^2$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$[72,88]$
【解析】
不难得到 $A(8,0)$，$B(0,6)$，三角形 $OAB$ 的内切圆圆心为 $I(2,2)$，半径为 $2$．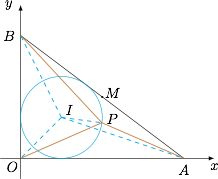
注意到$$\overrightarrow{PA}=\overrightarrow{PI}+\overrightarrow{IA}, $$从而有$$PA^2=PI^2+IA^2+2\overrightarrow{PI}\cdot\overrightarrow{IA},$$进而可得$$z=3PI^2+{IA^2}+IB^{2}+IO^{2}+2\overrightarrow{PI}\cdot\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IO}\right)=80+2\overrightarrow{PI}\cdot (2,0),$$于是可得所求的取值范围是 $[72,88]$．
注意到$$\overrightarrow{PA}=\overrightarrow{PI}+\overrightarrow{IA}, $$从而有$$PA^2=PI^2+IA^2+2\overrightarrow{PI}\cdot\overrightarrow{IA},$$进而可得$$z=3PI^2+{IA^2}+IB^{2}+IO^{2}+2\overrightarrow{PI}\cdot\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IO}\right)=80+2\overrightarrow{PI}\cdot (2,0),$$于是可得所求的取值范围是 $[72,88]$．
题目
答案
解析
备注
