若实数 $x,y$ 满足 $x^2+y^2\leqslant 1$，则 $\left|2x+y-2\right|+\left|6-x-3y\right|$ 的最小值是 ．
【难度】
【出处】
2015年高考浙江卷（理）
【标注】
【答案】
$ 3 $
【解析】
由于 $\left|x+3y\right|\leqslant \sqrt{10}\cdot\sqrt{x^2+y^2}<6$，于是原式等于$$\left|2x+y-2\right|+6-x-3y=\begin{cases}x-2y+4,&2x+y-2\geqslant 0,\\-3x-4y+8,&2x+y-2<0.\end{cases}$$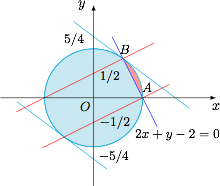
直线 $2x+y-2=0$ 将可行域 $x^2+y^2\leqslant 1$ 分割为两个弓形，其中 $A(1,0)$，$B\left(\dfrac 35,\dfrac 45\right)$．
对两个弓形分别进行线性规划可得取值范围分别为 $[3,5]$ 以及 $(3,13]$，因此所求代数式的取值范围为 $[3,13]$，最小值为 $3$．
直线 $2x+y-2=0$ 将可行域 $x^2+y^2\leqslant 1$ 分割为两个弓形，其中 $A(1,0)$，$B\left(\dfrac 35,\dfrac 45\right)$．对两个弓形分别进行线性规划可得取值范围分别为 $[3,5]$ 以及 $(3,13]$，因此所求代数式的取值范围为 $[3,13]$，最小值为 $3$．
题目
答案
解析
备注
