查看数据源：590abe9d6cddca000a081971
如图，圆 $C$ 与 $x$ 轴相切于点 $T(1,0)$，与 $y$ 轴正半轴交于两点 $A$、$B$（$B$ 在 $A$ 的上方），且 $AB=2$．$(1)$ 圆 $C$ 的标准方程为 ；
$(2)$ 过点 $A$ 任作一条直线与圆 $O:x^2+y^2=1$ 相交于 $M$、$N$ 两点，下列三个结论：
① $\dfrac{NA}{NB}=\dfrac{MA}{MB}$；
② $\dfrac{NB}{NA}-\dfrac{MA}{MB}=2$；
③ $\dfrac{NB}{NA}+\dfrac{MA}{MB}=2\sqrt 2$．
其中正确结论的序号是 ．（写出所有正确结论的序号）
【难度】
【出处】
2015年高考湖北卷（理）
【标注】
  • 知识点
    >
    解析几何
    >
    圆
    >
    圆的定义
    >
    阿波罗尼斯圆
  • 知识点
    >
    平面几何
    >
    相似三角形
  • 题型
    >
    解析几何
    >
    圆锥曲线的性质证明问题
  • 知识点
    >
    解析几何
    >
    圆
    >
    圆的方程
    >
    圆的标准方程
【答案】
$(1)$ $ (x-1)^2+\left(y-\sqrt 2\right)^2=2 $：$(2)$ ①②③
【解析】
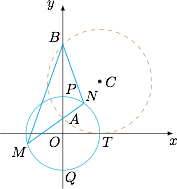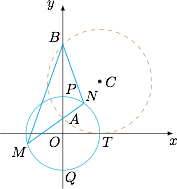$(1)$ 由于圆 $C$ 与 $x$ 轴相切于 $(1,0)$，于是弦 $AB$ 与圆心的距离为 $1$，进而可得圆的半径为 $\sqrt 2$，于是圆 $C$ 的方程为$$(x-1)^2+\left(y-\sqrt 2\right)^2=2.$$$(2)$ 点 $A\left(0,\sqrt 2-1\right)$，点 $B\left(0,\sqrt 2+1\right)$，设圆 $O$ 与 $y$ 轴的交点分别为 $P$、$Q$，如图．由于$$\overrightarrow{AP}=\left(\sqrt 2-1\right)\overrightarrow{PB},\\\overrightarrow{AQ}=-\left(\sqrt 2-1\right)\overrightarrow{QB},$$于是以 $PQ$ 为直径的圆 $O$ 上的点到 $A$ 与到 $B$ 的距离之比$$\dfrac{MA}{MB}=\dfrac{NA}{NB}=\sqrt 2-1,$$因此命题 ①②③ 均正确．
题目 答案 解析 备注
0.128876s