设函数 $f(x)$ 的定义域为 $D$，若存在非零实数 $l$ 使得对于任意 $x\in M$（$M\subseteq D$），有 $x+l\in D$，且 $f(x+l)\geqslant f(x)$，则称 $f(x)$ 为 $M$ 上的 $l$ 高调函数．现给出下列命题：
① 函数 $f(x)=\left(\dfrac 12\right)^x$ 为 $\mathbb R$ 上的 $1$ 高调函数；
② 函数 $f(x)=\sin 2x$ 为 $\mathbb R$ 上的 $\pi $ 高调函数；
③ 如果定义域为 $\left[-1,+\infty\right)$ 的函数 $f(x)=x^2$ 为 $\left[-1,+\infty\right)$ 上的 $m$ 高调函数，那么实数 $m$ 的取值范围是 $\left[2,+\infty\right)$．
其中正确的命题是 ．
① 函数 $f(x)=\left(\dfrac 12\right)^x$ 为 $\mathbb R$ 上的 $1$ 高调函数；
② 函数 $f(x)=\sin 2x$ 为 $\mathbb R$ 上的 $\pi $ 高调函数；
③ 如果定义域为 $\left[-1,+\infty\right)$ 的函数 $f(x)=x^2$ 为 $\left[-1,+\infty\right)$ 上的 $m$ 高调函数，那么实数 $m$ 的取值范围是 $\left[2,+\infty\right)$．
其中正确的命题是
【难度】
【出处】
无
【标注】
【答案】
②③
【解析】
先去理解所谓 $l$ 高调函数的含义．
首先单调递增函数必然是 $l$ 高调函数（$l>0$），单调递减函数必然不是高调函数．那么函数有增有减时，情况是什么样的呢？
从图形上来看，$l$ 高调函数应该主体上是单调递增的，且由于递减产生的“坑”的宽度应该不超过 $l$．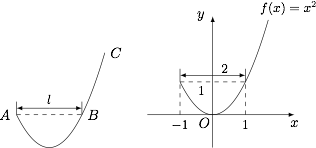
① $f(x)$ 单调递减，不正确；
② 因为 $f(x+\pi)=f(x)$，正确；
③ 若 $f(x)=x^2$ 为 $[-1,+\infty)$ 上的 $m$ 高调函数，则 $m \geqslant 2$，正确．
首先单调递增函数必然是 $l$ 高调函数（$l>0$），单调递减函数必然不是高调函数．那么函数有增有减时，情况是什么样的呢？
从图形上来看，$l$ 高调函数应该主体上是单调递增的，且由于递减产生的“坑”的宽度应该不超过 $l$．
① $f(x)$ 单调递减，不正确；② 因为 $f(x+\pi)=f(x)$，正确；
③ 若 $f(x)=x^2$ 为 $[-1,+\infty)$ 上的 $m$ 高调函数，则 $m \geqslant 2$，正确．
题目
答案
解析
备注
