若函数 $f(x)=|x+1|+2|x-a|$ 的最小值为 $5$，则实数 $a=$ ．
【难度】
【出处】
2015年高考重庆卷（理）
【标注】
【答案】
$4$ 或 $-6$
【解析】
先回顾一个我们较为熟悉的函数 $g(x)=|x+1|+|x-a|$，其函数值的几何意义为数轴上表示 $x$ 的点到表示 $-1$ 和 $a$ 的点的距离之和，函数图象以 $x=\dfrac{-1+a}2$ 为对称轴，如图所示．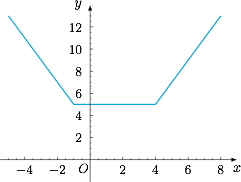
接下来思考，如果这个函数再加上另一个函数 $h(x)=|x-a|$，对函数的图象会造成什么样的影响？
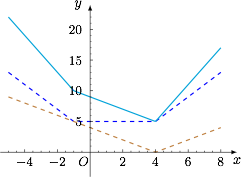如图，函数 $h(x)$ 的加入会使得函数图象在 $x=a$ 处“下沉”（图中 $a>-1$，但并不影响本质），于是函数 $f(x)$ 在 $x=a$ 处取得最小值，所求 $a$ 的值可以由$$|a+1|=5$$解得．
当然，也可以采用如下的代数描述：根据已知，有\[f(x)\geqslant \left|(x+1)-(x-a)\right|+|x-a|=|1+a|+|x-a|\geqslant |1+a|,\]等号当 $x=a$ 时取得．以下略．
接下来思考，如果这个函数再加上另一个函数 $h(x)=|x-a|$，对函数的图象会造成什么样的影响？如图，函数 $h(x)$ 的加入会使得函数图象在 $x=a$ 处“下沉”（图中 $a>-1$，但并不影响本质），于是函数 $f(x)$ 在 $x=a$ 处取得最小值，所求 $a$ 的值可以由$$|a+1|=5$$解得．当然，也可以采用如下的代数描述：根据已知，有\[f(x)\geqslant \left|(x+1)-(x-a)\right|+|x-a|=|1+a|+|x-a|\geqslant |1+a|,\]等号当 $x=a$ 时取得．以下略．
题目
答案
解析
备注
