查看数据源：590ac27f6cddca000a0819a1
已知函数 $f\left( x \right) = \left|{{x^2}+ 3x}\right|$，$x \in{\mathbb{R}}$．若方程 $f\left( x \right) - a\left|{x - 1}\right| = 0$ 恰有 $4$ 个互异的实数根，则实数 $a$ 的取值范围为 ．
【难度】
【出处】
2014年高考天津卷（理）
【标注】
  • 方法
    >
    代数处理
    >
    分离变量法
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    分式函数
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的零点
【答案】
$(0,1)\cup(9,+\infty )$
【解析】
显然 $x=1$ 不是方程的根，因此题中方程即$$a=\left|\dfrac{x^2+3x}{x-1}\right|,$$令 $x-1=t$，则上述方程即$$a=\left|t+\dfrac 4t+5\right|,$$也即$$t+\dfrac 4t=a-5\lor t+\dfrac 4t=-a-5,$$其中 $a\geqslant 0$．于是题意即函数 $y=t+\dfrac 4t$ 的图象与直线 $y=a-5$ 和直线 $y=-a-5$ 均有两个公共点（这里利用了函数 $y=t+\dfrac 4t$ 图象的特点），如图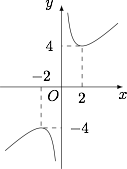．因此有$$\begin{cases} a>0,\\-a-5<-4,\\ a-5<-4\lor a-5>4,\end{cases}$$解得 $0<a<1$ 或 $a>9$，因此实数 $a$ 的取值范围是 $(0,1)\cup(9,+\infty )$．
题目 答案 解析 备注
0.109284s