已知偶函数 $f(x)$ 满足 $f(x+2)=\dfrac{1}{f(x)}$，且当 $x\in [1,2)$ 时，$f(x)=x-2$，则 $f(6.5)=$ ．
【难度】
【出处】
无
【标注】
【答案】
$-0.5$
【解析】
已知条件描述了 $f(x)$ 的两个性质：
① 自变量互为相反数时函数值可以互相推导；
② 自变量差为 $2$ 时函数值可以互相推导．
于是问题转化成了如何将自变量 $6.5$ 转化到已知函数解析式的自变量的取值范围 $[1,2)$ 上．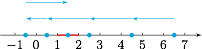
如图，一个可行的路径为$$6.5\to 4.5\to 2.5\to 0.5\to -0.5\to 1.5,$$于是对应的书写为$$f(6.5)=\dfrac{1}{f(4.5)}=f(2.5)=\dfrac{1}{f(0.5)}=\dfrac{1}{f(-0.5)}=f(1.5)=1.5-2=-0.5.$$
① 自变量互为相反数时函数值可以互相推导；
② 自变量差为 $2$ 时函数值可以互相推导．
于是问题转化成了如何将自变量 $6.5$ 转化到已知函数解析式的自变量的取值范围 $[1,2)$ 上．
如图，一个可行的路径为$$6.5\to 4.5\to 2.5\to 0.5\to -0.5\to 1.5,$$于是对应的书写为$$f(6.5)=\dfrac{1}{f(4.5)}=f(2.5)=\dfrac{1}{f(0.5)}=\dfrac{1}{f(-0.5)}=f(1.5)=1.5-2=-0.5.$$
题目
答案
解析
备注
